1703625065
对于大多数的情景来说,链接方法的选择通常不会改变结果的解释。我偏爱几何法超额收益率,所以我更愿意采用几何法链接。对于算术法超额收益率,我更喜欢GRAP法或Frongello法。
1703625066
1703625067
超额收益率的年化
1703625068
1703625069
就像投资组合收益率和参考基准收益率一样,超额收益率也能够(和应该)被年化。几何法超额收益率对于多时段可以自然地被复利化,但算术法超额收益率无法做到这一点。我们在表2-24的数据中引入了参考基准数据和相应的超额收益率数据,具体如表8-20所示。
1703625070
1703625071
表8-20 年化的超额收益率
1703625072
1703625073


1703625074
1703625075
1703625076
归因分析年化
1703625077
1703625078
使用式(6-23)来扩展式(8-26)以包括货币影响:
1703625079
1703625080
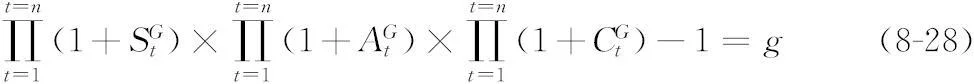
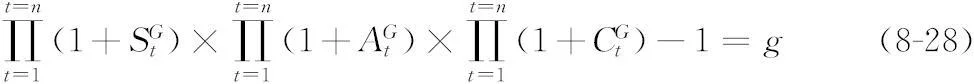
1703625081
1703625082
1703625083


1703625084
式中 ——时段t的总货币几何法归因影响。
1703625085
1703625086
所以,我们可以通过年化的股票选择贡献、资产配置贡献和货币贡献来复利化得到年化的几何法超额收益率,具体如表8-21所示。几何法超额收益率是内部一致的,所以可以在多时段年化。随着分析时段的延长,Carino法和Menchero法所带来的系统性剩余分布变得越来越不吸引人,而几何法复利化变得越来越吸引人。
1703625087
1703625088
表8-21 年化贡献得到超额收益率
1703625089
1703625090


1703625091
1703625092
1703625093
1703625094
1703625095
1703625096
投资组合绩效测评实用方法(原书第2版) [:1703619340]
1703625097
投资组合绩效测评实用方法(原书第2版) 第9章 归因分析问题的扩展
1703625098
1703625099
科学的一半是提出正确的问题。
1703625100
1703625101
罗杰·培根(Roger Bacon)(1214——1294)
1703625102
1703625103
1703625104
1703625105
1703625106
投资组合绩效测评实用方法(原书第2版) [:1703619341]
1703625107
投资组合绩效测评实用方法(原书第2版) 归因分析的变形
1703625108
1703625109
Brinson模型仍是绩效归因分析方法的基础,但它有很多形式的变形,同时还存在其他归因分析方法。
1703625110
1703625111
贡献分析(或绝对收益归因分析)
1703625112
1703625113
没有参考基准或以绝对收益为目标的投资组合不适合采用绩效归因分析,因为它们没有基准来比较。贡献分析简单地将投资组合的收益率分解为单独投资工具或工具类型的贡献,从而提供了投资收益来源的一些信息。
1703625114