1704637975
1704637976
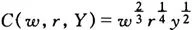
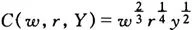
1704637977
12.函数可以成为一个成本函数吗?(这里w为工资率,r是利率,y为产量。)并请陈述你的理由。
1704637978
1704637979
13.推导成本函数C(r1,r2,q),当生产函数分别为以下形式时:
1704637980
1704637981
(1)f(z1,z2)=z1+z2
1704637982
1704637983
(2)f(z1,z2)=min{z1,z2}
1704637984
1704637985


1704637986
(3)
1704637987
1704637988
注:假设每个生产函数都只有一种产出。z1、z2为两种投入,r1、r2分别为两种投入的单价,q为产量。
1704637989
1704637990
14.下列说法对吗?为什么?
1704637991
1704637992
(1)当边际成本(MC)下降时,平均成本必下降;
1704637993
1704637994
(2)当边际成本(MC)上升时,平均成本必上升。
1704637995
1704637996
15.对于生产函数f(z1,z2)=a1lnz1+a2lnz2(a1>0,a2>0),计算利润最大化的利润函数、供给函数。并判断该利润函数是否满足课本上讲过的性质(1)—(4)。
1704637997
1704637998
注:假设该生产函数只有一种产出。z1、z2为两种投入。
1704637999
1704638000
16.证明:“在竞争型的市场中,如果一个厂商的生产技术具有规模报酬不变的特性,那么如果最大利润存在,它一定为零。”
1704638001
1704638002
17.说明生产者剩余也能由如下运算得出
1704638003
1704638004


1704638005
1704638006
1704638007
这里,p*是市场给出的价格,企业是价格接受者。
1704638008
1704638009
18.假定一个从事非法复制计算机CDs的厂商有如下每日短期总成本函数
1704638010
1704638011
STC=q2+25
1704638012
1704638013
(1)如果非法复制的计算机CDs每盘卖20元,则这个厂商每天生产多少?它的利润是多少?
1704638014
1704638015
(2)当p=20美元时,厂商的短期生产者剩余是多少?
1704638016
1704638017
(3)写出这个厂商的生产者剩余作为非法CDs价格的函数的一般表达式。
1704638018
1704638019
19.给出下列论断不成立的反例(或图像):
1704638020
1704638021
(1)平均成本在任何地方都递减意味着边际成本在任何地方都递减。
1704638022
1704638023
(2)成本函数呈次可加性意味着平均成本在任何地方都递减。
1704638024