1700976577
力学(物理类) [:1700973453]
1700976578
力学(物理类) 2.5 动量定理
1700976579
1700976580
2.5.1 动量定理
1700976581
1700976582
作用于质点的力,在时间上的累积量称为力的冲量,导致的力学效应是质点的动量发生变化.
1700976583
1700976584
质量为m的质点,在某惯性系的速度为v,相对此惯性系的动量定义为
1700976585
1700976586


1700976587
1700976588
1700976589
质点所受力F,经dt时间提供的冲量定义为
1700976590
1700976591


1700976592
1700976593
1700976594
在t1到t2时间内提供的冲量便是
1700976595
1700976596


1700976597
1700976598
1700976599
质点所受力F可由若干分力Fi合成,即有
1700976600
1700976601


1700976602
1700976603
1700976604
那么合力冲量应等于分力冲量之和,即
1700976605
1700976606
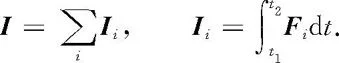
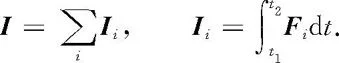
1700976607
1700976608
1700976609
据牛顿第二定律可得
1700976610
1700976611


1700976612
1700976613
1700976614
即力(合力)为质点提供的冲量等于质点的动量增量,这就是质点动量定理.
1700976615
1700976616
质点系的动量p定义为各质点动量pi之和,即有
1700976617
1700976618


1700976619
1700976620
1700976621
将质点系各质点所受力分为内力与外力两类,内力指这些质点之间的相互作用力,外力指质点系外的物体或物质提供的力.内力冲量之和记为I内,外力冲量和记为I外,则有
1700976622
1700976623


1700976624
1700976625
1700976626
据牛顿等三定律,任何一对作用力、反作用力冲量和必为零,得