1700947950

1700947951
1700947952
1700947953
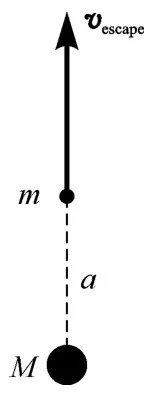
图3-3 距离质量为M的物体a处的逃逸速度
1700947954
1700947955
现在,这是在半径a 处的逃逸速度公式。但是假定速度va 是任意的,而我们来求由va 表示的b 。能量守恒告诉我们,质点在近日点的动能和势能必定等于它在远日点的动能和势能——这样我们就能利用它来计算b ,一眼就看出:
1700947956
1700947957


1700947958
1700947959
1700947960
Infelizmente [1] ,我们却没有vb ,所以除非存在某种外部机制或者经分析而得出vb ,否则我们永远无法从(3.2)式求出b 。
1700947961
1700947962
但是如果我们记得开普勒的等面积定律,那么我们就知道,在给定的时间间隔内,在远日点扫过的面积和在近日点扫过的面积相等;在短时间间隔Δt 内,质点在近日点通过距离va Δt ,所以它扫过的面积约为a ·va Δt /2,而在远日点,质点经过的距离vb Δt ,扫过的面积约为bvb Δt /2,“面积相等”意指ava Δt /2等于bvb Δt /2——这意味着速度与半径反比地变化(见图3-4)。
1700947963
1700947964


1700947965
1700947966
1700947967


1700947968
1700947969
1700947970
图3-4 利用开普勒等面积定律求卫星在远日点的速度
1700947971
1700947972
于是,上式给了我们由va 表示的vb 的公式。我们可以将其代入(3.2)式。因而我们就有一个确定b 的方程:
1700947973
1700947974


1700947975
1700947976
1700947977
两边除以m ,再重新排列,我们得
1700947978
1700947979


1700947980
1700947981
1700947982


1700947983


1700947984
你若仔细看一下(3.5)式,可能会说“好,我可以用b2 去乘,于是上式就变为b 的二次方程。”或者,如果你们喜欢,就像原来这样,解 的二次方程——两种方法都行。 的解为:
1700947985
1700947986


1700947987
1700947988
1700947989
此后我不再讨论这个代数式;你们知道如何解二次方程,并且b 存在两个解:可以发现其中一个解是b 等于a ——这令人高兴,因为如果你们考察(3.2)式就会看到,显然b 等于a 时方程将相等。(这意味着b 就是a 。)根据另一个解,得到用a 表示的b 的公式,把它写下:
1700947990
1700947991


1700947992
1700947993
1700947994
现在的问题是,我们是否可用这样的方式来写上式,即使得va 与距离a 处的逃逸速度的关系能够明显看出。注意到由(3.1)式,2GM /a 就是逃逸速度的平方,所以我们可把上式写成如下形式:
1700947995
1700947996


1700947997
1700947998
1700947999
这就是最后的结果,相当有意思,首先假定va 小于逃逸速度。在这种情况下,我们预料质点不会逃逸,所以我们会得到合理的b 值。果然,要是va 小于vesc ,则vesc /va 大于1,其平方也大于1,减去1,你们就得到某个合理的位置数值,a 除以该数就告诉我们b 。