1700978909
1700978910
图 4-5
1700978911
1700978912
略去一颗行星受其他天体的作用,只计及太阳的引力,行星在沿椭圆轨道运动过程中相对于太阳的角动量守恒,从太阳向行星引出的径矢在单位时间内扫过的面积便是常量,这就是开普勒第二定律(面积定律).设想某个小行星意外获得较高的动能,使它有可能相对太阳作抛物线或双曲线运动,此时面积定律仍然成立.行星在轨道运动中,若选太阳之外的任何其他参考点,角动量都不会守恒.
1700978913
1700978914
例1 圆锥摆的辐角为θ,摆线长为l,摆球质量为m,取悬挂点O为参考点,试求摆球所受力的力矩M和摆球角动量L.
1700978915
1700978916
解 如图4-6所示,摆球受摆线张力T与重力mg,前者相对O点力矩为零,故
1700978917
1700978918


1700978919
1700978920
1700978921


1700978922
1700978923
1700978924
图 4-6
1700978925
1700978926
摆球圆运动向心力由T与mg合成,可算得
1700978927
1700978928


1700978929
1700978930
1700978931
故
1700978932
1700978933
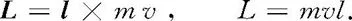
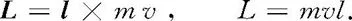
1700978934
1700978935
1700978936
图4-6示出了摆球在某一位置时M和L的方向.摆球运动时,M,L随摆球绕圆心O旋转.L的竖直分量L⊥恒定不变,这与M的竖直分量恒为零相符.L的水平分量L∥与M类似,均为水平旋转矢量.
1700978937
1700978938
例2 导出单摆的摆动方程.
1700978939
1700978940
解 单摆的有关参量已在图4-7中给出,设置垂直于图平面朝外的水平z轴,T+mg相对悬挂点O的力矩M仅有z轴分量,可得
1700978941
1700978942


1700978943
1700978944
1700978945


1700978946
1700978947
1700978948
图 4-7
1700978949
1700978950
角动量L也仅有z轴分量,可得
1700978951
1700978952


1700978953
1700978954
1700978955
据Mz=dLz/dt,有-mgl sinθ=ml2d2θ/dt2,或表述成
1700978956
1700978957


1700978958