1700979382
1700979383
1700979384
图 4-21
1700979385
1700979386
即等于球体质量集中于球心处所受外引力FO相对Q点力矩与球体各部位外引力相对球心O的力矩之和.图4-21中虽将参考点Q取在球外,其实上述论述同样适用于Q在球体内的情况.
1700979387
1700979388
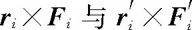
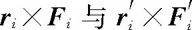
1700979389
再设球外仅有一个外质点P,球内任一小部位i在i,P,O确定的平面上,总可唯一地取到图4-22所示的对称小部位i′.参考图示参量,显然等值且反向,故有
1700979390
1700979391


1700979392
1700979393
1700979394


1700979395
1700979396
1700979397
图 4-22
1700979398
1700979399
对称球可分解成一系列这样的对称小部位,得
1700979400
1700979401
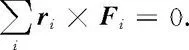
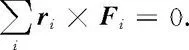
1700979402
1700979403
1700979404
如果对称球外有若干外质点,它们对球体施加的外引力可分解成单个外质点单独提供的外引力之和,因此上式对多个外质点情况仍然成立.
1700979405
1700979406
综上所述,可得
1700979407
1700979408
(1)对称球外引力相对球心力矩之和为零;
1700979409
1700979410
(2)对称球外引力相对任一参考点Q的力矩之和,等于球体质量集中于球心处所受外引力相对Q点的力矩.
1700979411
1700979412
1700979413
1700979414
1700979415
力学(物理类) [:1700973463]
1700979416
力学(物理类) 4.2 对称性与守恒律
1700979417
1700979418
4.2.1 对称性
1700979419
1700979420
自然界中某些事物对半分开后,向左、向右或向上、向下的结构相同,前者如人体外观,后者如水面上下景像.这些感觉在人的思维中形成了对称的原始观念.左右对称既具有简单的和谐与朴素的美感,又易于创作,更多地表现在古建筑中.我国历代自民间屋宇、城墙门楼到帝王宫殿,几乎都是左右对称的.汉字中“门”的繁体字“門”取象形结构,也成左右对称.欧洲人同样欣赏这种简朴的对称,刻意编制的语句“Madam, I’m Adam”,以“I”中分,左右对称,可以从左边开始念,也可以从右边开始念,内容相同.左右对称,上下对称都可以通过平面镜物像关系来比喻,所以也称镜面对称.
1700979421
1700979422
为尝试用科学的语言表述镜面对称,取两个相同的几何圆锥体,如图4-23所示,对称地放在yz平面的两侧.设想yz平面上有一面镜(图中用虚线画出),两个锥体便呈物像关系.以这两个锥体构成的系统作为考察对象,不难发现,全系统中每一个点部位的坐标量x置换成-x,保持y,z不变,所得新系统与原系统相同.数学上将仅取x到-x(或y到-y,或z到-z)的变换称为镜面反演,于是一个系统若在镜面反演变换下保持不变,那么称这一系统具有镜面反演对称性.
1700979423
1700979424


1700979425
1700979426
1700979427
图 4-23
1700979428
1700979429
将对称性精练地定义为系统在某种变换下具有的不变性,是德国数学家魏尔(H. Weyl)首先提出的.镜面反演属于空间变换,此外,还有时间变换和其他各种变换.力学讨论质点系运动状态的变化以及其中的动力学规律,这些内容都可以构成系统,考察它们在空间、时间各种变换下所具有的对称性.
1700979430
1700979431
●空间变换对称性