1700979601
1700979602
历史上正是这些实验定律帮助牛顿发现了他的万有引力定律(本章例16将给出牛顿万有引力定律一种简化的导出方案).反之,也可以在牛顿力学范畴内结合引力定律,借助两体引力系统,从理论上导得开普勒三定律.
1700979603
1700979604
在某太空惯性系中已将太阳处理成不动的质点,因此这一太空惯性系可等效地称为日心参考系,或不计自转的太阳参考系.将太阳质量记为M,待考察的行星质量记为m.某时刻在M至m的径矢r和m的速度v确定的平面上,建立以M为原点的极坐标系,如图4-32所示.m所受引力
1700979605
1700979606


1700979607
1700979608
1700979609


1700979610
1700979611
1700979612
图 4-32
1700979613
1700979614
也在此平面上.确定m而后运动的原因都在这一平面内,平面两侧空间相对该平面具有镜面对称性,m的运动须保持这样的对称性,即m的运动轨道必定是该平面中的一条曲线.平面极坐标系中m的轨道曲线可表述成r-θ函数,这一函数可由m的径向速度vr,角向速度vθ与dr/dθ间的下述关系来导得:
1700979615
1700979616


1700979617
1700979618
1700979619
m运动过程中相对于M的角动量L守恒,能量E守恒,即有
1700979620
1700979621


1700979622
1700979623
1700979624
首先可得
1700979625
1700979626


1700979627
1700979628
1700979629
继而可得
1700979630
1700979631


1700979632
1700979633
1700979634
引入参量
1700979635
1700979636


1700979637
1700979638
1700979639
则有
1700979640
1700979641
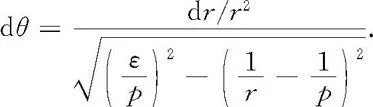
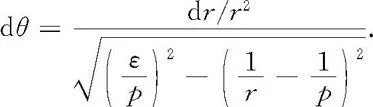
1700979642
1700979643
1700979644


1700979645


1700979646
引入变量,则,有
1700979647
1700979648


1700979649
1700979650