1700983532
1700983533
考虑到算符 内含的微商运算会丢失可能有的常量差,宜将p(r)与εp(r)之间的关系表述为
1700983534
1700983535


1700983536
1700983537
1700983538
式中p0为待定常量.
1700983539
1700983540
算例 盛放在桶内的液体随桶绕着中央竖直轴以恒定的角速度ω旋转,以桶为参考系,设置图6-12所示的Oxyz坐标系.以z=0为重力势能零点,(x,y,z)处液体的势能密度为
1700983541
1700983542


1700983543
1700983544
1700983545


1700983546
1700983547
1700983548
图 6-12
1700983549
1700983550
其中ρ是液体密度.(x,y,z)处液体的压强便是
1700983551
1700983552
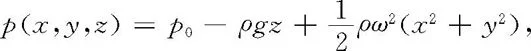
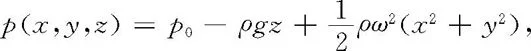
1700983553
1700983554
1700983555
其中p0为z=0处液体压强.在x=0,y=0,z=z0处,液体压强等于大气压强pa,便有
1700983556
1700983557


1700983558
1700983559
1700983560
则
1700983561
1700983562


1700983563
1700983564
1700983565
液体表面压强均为pa,液体表面方程为
1700983566
1700983567


1700983568
1700983569
1700983570
即
1700983571
1700983572


1700983573
1700983574
1700983575
例3 密度为ρ0的液体在容器的下部,密度为ρ0/3的液体在容器的上部,两种流体互不溶合.高H、密度为ρ0/2的长方固体静止在液体中,如图6-13所示,试求图中两个高度量h1与h2.
1700983576
1700983577


1700983578
1700983579
1700983580
图 6-13
1700983581