1700984758
图 7-1
1700984759
1700984760
称这种方式的振动为简谐振动,(7.1)式便是简谐振动的运动方程.t时刻质点速度v和加速度a也在图中示出,x方向简谐振动的速度和加速度分别是
1700984761
1700984762


1700984763
1700984764
1700984765
(7.2)和(7.3)式也可通过(7.1)式对t求导获得.
1700984766
1700984767
无地面摩擦和空气阻力时,水平弹簧振子的位置量x随时间t的变化关系与(7.1)式相同,无空气阻力时,小角度单摆的角位置量θ随时间t的变化关系也与(7.1)式相同,它们的运动也都是简谐振动.
1700984768
1700984769
简谐振动的x-t图线称为振动曲线,它是数学中的余弦曲线,如图7-2所示.据(7.1)式,有
1700984770
1700984771
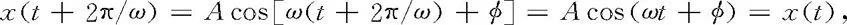
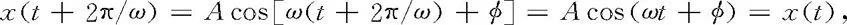
1700984772
1700984773
1700984774


1700984775
1700984776
1700984777
图 7-2
1700984778
1700984779
可见简谐振动是周期为
1700984780
1700984781


1700984782
1700984783
1700984784
的运动,称
1700984785
1700984786


1700984787
1700984788
1700984789
为振动频率,称
1700984790
1700984791


1700984792
1700984793
1700984794


1700984795


1700984796


1700984797
为角频率.在一个周期内,x可从A→-A→A变化一次,称A为振幅.(7.1)式显示,位置x随时间t的变化关系可表现为位置x由参量ωt+确定,称ωt+为t时刻振动的相位,称为振动的初相位.
1700984798
1700984799
7.1.2 同方向同频率简谐振动的合成
1700984800
1700984801
一个质点如果同时参与两个同方向同频率的简谐振动:
1700984802
1700984803


1700984804
1700984805
1700984806
那么它的合振动应为
1700984807