1700985782


1700985783
1700985784
1700985785
滚动周期便是
1700985786
1700985787


1700985788
1700985789
1700985790
例11 在一竖直方向线上有两个固定的水平光滑细钉,相距l,一圈长度略大于2l的细绳如图7-29所示套在这两个细钉外侧,右半圈绳的质量线密度为常量λ,左半圈绳的质量线密度为2λ.开始时绳静止,而后自由释放,绳圈将会形成无摩擦的周期性往返运动,试求周期T.
1700985791
1700985792


1700985793
1700985794
1700985795
图 7-29
1700985796
1700985797
解 参考图7-30,左半圈绳的上端P下落高度为x时,机械能守恒式为
1700985798
1700985799


1700985800
1700985801
1700985802


1700985803
1700985804
1700985805
图 7-30
1700985806
1700985807
两边对t求导,可得
1700985808
1700985809


1700985810
1700985811
1700985812
引入新的参量
1700985813
1700985814
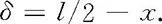
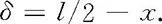
1700985815
1700985816
1700985817
可得
1700985818
1700985819


1700985820
1700985821
1700985822
这是简谐振动微分方程,因此δ,x均作简谐振动,振动周期为
1700985823
1700985824


1700985825
1700985826
1700985827
例12 如图7-31所示,劲度系数为k、质量为m的均匀水平弹簧一端固定,另一端连接质量为M的小球,小球与水平地面间无摩擦.让小球偏离平衡位置x=0点,自由释放后便可沿图示的x轴振动.在弹簧无形变时,以固定端为原点沿弹簧设置向右的ξ坐标.设小球振动量为x时,弹簧中原ξ点的振动量(即相对其初始位置的位移量)为uξ=(ξ/l0)x,式中l0是弹簧自由长度.这一假设也可简单地说成:弹簧各处振动量与小球振动量成正比.作此假设后,试求小球振动周期T.
1700985828
1700985829


1700985830
1700985831