1700986532
1700986533
据(7.59)式,振动速度为
1700986534
1700986535


1700986536
1700986537
1700986538
设t=0时,x=x0,vx=v0,则有
1700986539
1700986540


1700986541
1700986542
1700986543
解得
1700986544
1700986545


1700986546
1700986547
1700986548


1700986549


1700986550
所在象限还需参考cos=x0/A的正负号来判定.
1700986551
1700986552


1700986553
低阻尼振动图线如图7-45所示,振子仍在x=0点两侧往返振动,但是阻尼力使振动减慢,这表现为角频率从ω0减至,振动周期相应地从2π/ω0增大到T=2π/ω.阻尼力同时使振动幅度以Ae-βt方式随时间呈指数衰减.常将t时刻振幅与t+T时刻振幅之比的自然对数称为对数减缩,记为λ,有
1700986554
1700986555
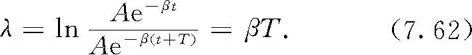
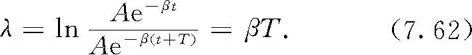
1700986556
1700986557
1700986558


1700986559
1700986560
1700986561
图7-45 低阻尼
1700986562
1700986563


1700986564


1700986565
从能量方面考察,振子动能,势能都与振幅Ae-βt有关,使得振子机械能E也随时间呈指数衰减.单位时间内E的增量(为负值)
1700986566
1700986567


1700986568
1700986569
1700986570


1700986571
因,即得
1700986572
1700986573


1700986574
1700986575
1700986576
可见E的减少是由于阻尼力提供了负的功率.
1700986577
1700986578
t时刻振子能量记为E,经过一个周期,振子损失的能量记为∆E,则耗能百分比为∆E/E.从能耗方面引入称之为品质因数Q的量,定义为
1700986579
1700986580


1700986581