1700986843
1700986844
(1)无论ω为何值,每一周期内驱动力作功量恰好与阻尼力作功量相互抵消;
1700986845
1700986846
(2)当ω=ω0时,每一时刻驱动力功率与阻尼力功率相互抵消.
1700986847
1700986848
证 受迫振动达稳定态时,据(7.74)式,振动速度为
1700986849
1700986850


1700986851
1700986852
1700986853


1700986854
其中sin参考本章例20解答过程,可导得为
1700986855
1700986856


1700986857
1700986858
1700986859
据(7.68)式又可得
1700986860
1700986861


1700986862
1700986863
1700986864
②代入①后,考虑到2β=γ/m,f0=F0/m,便有
1700986865
1700986866


1700986867
1700986868
1700986869
(1)一个周期内驱动力作功量为
1700986870
1700986871


1700986872
1700986873
1700986874
一个周期阻尼力作功量为
1700986875
1700986876
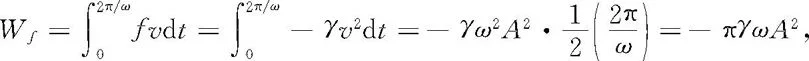
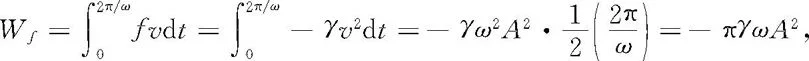
1700986877
1700986878
1700986879
可见WF与W∫相互抵消.
1700986880
1700986881
(2)驱动力功率和阻尼力功率分别为
1700986882
1700986883


1700986884
1700986885
1700986886
任意t时刻,未必有PF+P∫=0.ω=ω0时,则有
1700986887
1700986888


1700986889
1700986890
1700986891
可见每一时刻PF与P∫相互抵消.
1700986892