1700986932
1700986933
1700986934
必是①式特解.平移时间零点,即引入新的时间参量
1700986935
1700986936


1700986937
1700986938
1700986939
④式可改述成
1700986940
1700986941


1700986942
1700986943
1700986944
仿照(7.68)式,可解得
1700986945
1700986946


1700986947
1700986948
1700986949
综上所述,①式通解为
1700986950
1700986951


1700986952
1700986953
1700986954


1700986955


1700986956
其中x0(t)为阻尼通解,An和n由⑤式给出,ωn和0n及f0n由②、③式给出.
1700986957
1700986958


1700986959
例23 如图7-52所示,长l、质量m、带电量q>0的小角度单摆,摆动过程中受空气阻力f=-γv,在摆动平面上有水平方向交变电场E=E0cosωt,其中E0为小量,且有,试求单摆的稳态解.
1700986960
1700986961


1700986962
1700986963
1700986964
图 7-52
1700986965
1700986966
解 以悬挂点为参考点,单摆的角动量方程为
1700986967
1700986968


1700986969
1700986970
1700986971
θ为小角度时,近似有
1700986972
1700986973


1700986974
1700986975
1700986976
这一受迫振动方程的稳态解为
1700986977
1700986978
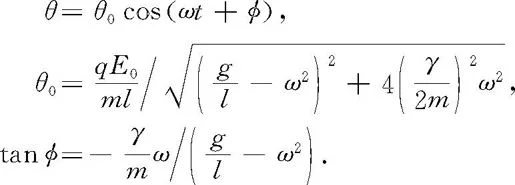
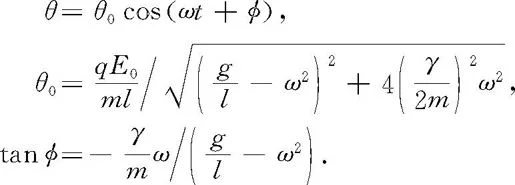
1700986979
1700986980
1700986981

