1700987193
显然,∆P=2kπ时AP=A1+A2为最大,∆P=(2k+1)π时AP=∣A1-A2∣为最小.如果1,2恒定,那么AP的大小由r1,r2确定,即由P点的空间位置确定,出现了干涉现象.波源S1,S2的初相位1,2恒定,确保了AP的大小仅由r1,r2确定,如果1,2经常变化,AP的大小会因受1-2的影响而随时间变化,破坏了干涉现象.在某些波源S1,S2中,虽然1,2会随时间变化,但仍能保持1-2恒定,同样也可产生干涉现象.
1700987194
1700987195
取两列振幅相同的相干平面简谐波,假设分别沿x轴正、负方向传播,即有
1700987196
1700987197
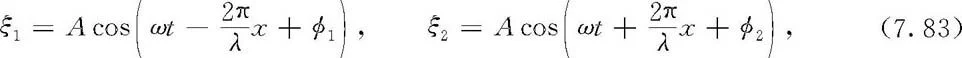
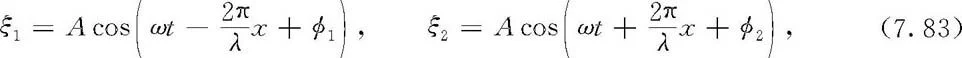
1700987198
1700987199
1700987200
相干叠加后,x处的合振动为
1700987201
1700987202


1700987203
1700987204
1700987205
平移x轴的坐标原点和时间零点,即引入x′和t′,使得
1700987206
1700987207


1700987208
1700987209
1700987210
则
1700987211
1700987212


1700987213
1700987214
1700987215


1700987216
(7.85)式表明,各x′处振动量ξ随时间t′按cosωt′规律同步变化,带有正负号的“振幅”随空间位置x′周期性地变化,空间周期为λ.“振幅”的绝对值,即真正意义下的振幅,其空间周期则为λ/2.从t′=0的波形曲线1到t′=T/2的波形曲线5,变化情况如图7-63所示.这样的两列行波相干叠加后合成的波不再右行或左行,而是在原地上下“踏步”,称之为驻波.驻波中振幅为零处称为波节,振幅最大处称为波腹.相邻波节或相邻波腹的间距同为λ/2,相邻波节、波腹间距为λ/4.
1700987217
1700987218


1700987219
1700987220
1700987221
图 7-63
1700987222
1700987223
例26 琴弦中反射波的半波损,驻波中的振动模式.
1700987224
1700987225
小提琴的琴弦两端固定,用弓拉动琴弦的某个小部位,使得该部位形成自激振动,振动状态沿琴弦传播形成行波,再经两端反射出现反向行波.反射波的振幅与入射波的振幅几乎相同,但是π值的相位突变,使得两端点合振动为零,同时在弦上出现驻波,两个端点均为波节.
1700987226
1700987227
琴弦固定端反射波的π相位突变,也可折合成半个波长的波程损失,因此将这样的反射波说成有半波损.
1700987228
1700987229
驻波中的振动频率未必唯一,分别记为νn,但各自在琴弦上形成同种类型的机械波,其波速u相同,波长便分别为
1700987230
1700987231
λn=u/νn.
1700987232
1700987233
设弦长l,则有
1700987234
1700987235


1700987236
1700987237
1700987238
得
1700987239
1700987240


1700987241
1700987242