1700987657
1700987658
三、空气中的声波
1700987659
1700987660
空气中各部位之间只有挤压力,可以压缩,没有切向力,在空气中传播的声波是纵波.空气中的分子沿着波的传播方向振动,使得空气的密度和压强也随着时间变化,因此空气中的声波也可看作是密度波或者压强波.沿着某波线设置x轴,声波传播过程中,x处的空气截面会在它的基准位置(无声波时的位置)两侧振动,声波也可用该振动量ξ随x,t的变化来描述.
1700987661
1700987662
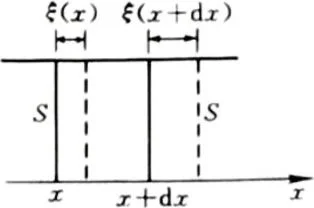
讨论沿x轴方向在截面积为S的空气柱中传播的声波.如图7-81所示,取x到x+dx小段,处在原位时,小段体积V=Sdx,压强设为p.t时刻x侧面有位移ξ(x,t),x+dx侧面有位移ξ(x+dx,t),压强变为p+dp,体积增为
1700987663
1700987664
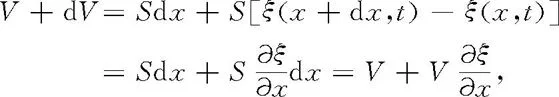
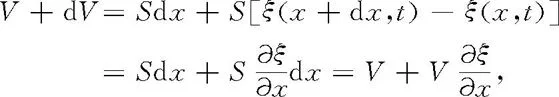
1700987665
1700987666
1700987667

1700987668
1700987669
1700987670
图 7-81
1700987671
1700987672
则有
1700987673
1700987674


1700987675
1700987676
1700987677
对于振动频率高于10Hz的声波,体积V的变化迅速,过程中气体间的热传导可略,即为绝热过程.将空气处理成理想气体,由热学理论可知绝热过程中变化的p,V间有下述关联:
1700987678
1700987679
pVγ=常量,
1700987680
1700987681
式中γ是由气体结构性质确定的常数,称为绝热指数.上式两边取微分,可得
1700987682
1700987683


1700987684
1700987685
1700987686
则
1700987687
1700987688


1700987689
1700987690
1700987691
如图7-82所示,在此空气柱中再取x到x+∆x小段,其中∆x仍是小量.无声波时,x侧面和x+∆x侧面处的压强同为p0,有声波时压强分别为
1700987692
1700987693


1700987694
1700987695
1700987696


1700987697
1700987698
1700987699
图 7-82
1700987700
1700987701
p(x),p(x+∆x)与p0差异很小,近似有
1700987702
1700987703


1700987704
1700987705
1700987706
空气柱的振动加速度∂2ξ/∂t2由两个侧面压力差提供,设无声波时的空气密度为ρ0,则有