1700987807
可见深水波的波速u与波长λ有关.不同波长的光在真空中传播速度相同,在某些介质(例如玻璃)中传播速度不同,这是白光通过三棱镜出现色散的原因.采用光学色散之说,称波速随波长变化的波为有色散的波.
1700987808
1700987809
将波长λ=2πu/ω或波数k=2π/λ代入(7.105)式,得
1700987810
1700987811


1700987812
1700987813
1700987814
可见有色散时,波速u会随角频率ω变化,或者说波速u会随波数k变化.
1700987815
1700987816
7.6.2 波动方程解
1700987817
1700987818
不同角频率的平面简谐波,无论右行或左行,都是一维线性波动方程(7.95)式的解.沿x正、负方向以相同波速u传播的任意平面波可以分解成一系列不同角频率相同波速的平面简谐波叠加,此类平面波构成(7.95)式通解.设波在x=0处的振动为
1700987819
1700987820


1700987821
1700987822
1700987823
若为右行波,x处t时刻的振动量同于x=0处t-x/u时刻的振动量,即得
1700987824
1700987825


1700987826
1700987827
1700987828
若为左行波,则有
1700987829
1700987830
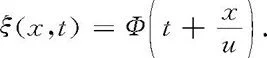
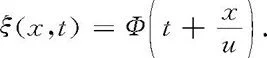
1700987831
1700987832
1700987833
据此,波动方程的通解可表述为
1700987834
1700987835


1700987836
1700987837
1700987838
其中Φ1,Φ2为任意形式函数.Φ1或Φ2可以是连续的,也可以是间断的,后者如图7-86所示的右行脉冲式波包,图中实线所示为t时刻波形,虚线所示为t+∆t时刻波形.
1700987839
1700987840


1700987841
1700987842
1700987843
图 7-86
1700987844
1700987845


1700987846


1700987847


1700987848


1700987849
简谐振动方程通解x=Acos(ωt+)中的两个待定常量A,,由t=0时刻的位置x0和速度v0确定.与此相似,可以理解波动方程通解(7.107)式中的两个待定函数Φ1和Φ2可由t=0时刻所有x点的振动量ξ(x,0)(其分布函数可记为F1(x))和振动速度(其分布函数可记为F2(x))确定.
1700987850
1700987851
7.6.3 色散和群速
1700987852
1700987853


1700987854


1700987855
单列平面简谐波的波形简单,波速u既是相位的传播速度,也是所有峰位的传播速度.若干列平面简谐波叠加后的波形曲线会变得复杂起来,尤其在角频率互异时更是如此.例如两列A,,u相同,ω1,ω2相近的平面简谐波叠加后,所得平面波为
1700987856