1700988493
7-46 如图7-110所示,一根线密度λm=0.15g/cm的弦线,其一端与频率ν=50Hz的音叉相连,另一端跨过定滑轮后悬一重物给弦线提供张力,音叉到滑轮间的距离l=1m.当音叉振动时,设重物不振动,为使弦上形成有一个、二个、三个波腹的驻波,则重物的质量m应各为多大?
1700988494
1700988495


1700988496
1700988497
1700988498
图 7-110(题7-46)
1700988499
1700988500


1700988501
7-47 已知弦线质量线密度为λ,弦中张力为T,弦中简谐横波的运动方程为试求弦波的能量线密度(单位长度上波的能量)ε.
1700988502
1700988503
B 组
1700988504
1700988505
7-48 两个同方向、不同频率的简谐振动,如果初相位相同,振幅不同,则可分别记为
1700988506
1700988507


1700988508
1700988509
1700988510
利用三角函数和差化积公式,这两个简谐振动的合振动可表述成
1700988511
1700988512


1700988513
1700988514
1700988515


1700988516
1700988517
1700988518
即可分解成两个拍的叠加.为方便称第一项为“大拍”,称第二项为“小拍”.由太阳引起的太阳潮和由月球引起的月亮潮,均可近似处理为简谐振动.太阳潮的振幅为0.5m,周期为12h(小时);月亮潮的振幅为0.8m,周期为12.5h.太阳潮与月亮潮合成的海水潮汐(海面振动)也可分解成两个拍的叠加,“大拍”达最大幅度A大时对应的潮汐称为大潮,“小拍”达最大幅度A小时对应的潮汐称为小潮.设海水足够深,试求A大,A小和相邻大潮与小潮之间的时间间隔∆t.
1700988519
1700988520
7-49 在一劲度系数为k的竖直轻长弹簧下端连接着质量为m的小球,开始时小球静止地处于力平衡态.设t=0时刻开始,弹簧上端以匀速度u竖直向上运动,到t=t0时刻又突然降速到零.建立附着于弹簧上端且竖直向下的x坐标轴,其原点选在t=0时刻小球所处位置,试在t≥0的范围确定小球位置x随时间t变化的函数关系.
1700988521
1700988522
7-50 图7-111所示的水平弹簧振子中,劲度系数为k的轻弹簧自由长度足够长.将质量为m的振子水平向右移动,直到弹簧伸长L,而后将振子自由释放.已知振子与水平地面间的摩擦因数为常量μ,试问若振子运动过程中至少停止过两次,那么第二次停留的位置相对振子的初始位置在何处?
1700988523
1700988524


1700988525
1700988526
1700988527
图 7-111(题7-50)
1700988528
1700988529
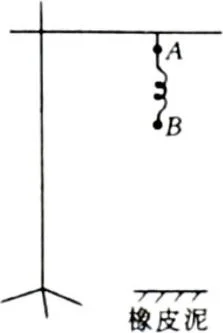
7-51 如图7-112所示,在水平地面上方高1m处有一固定的水平横杆,横杆下用细线悬挂着小球A,A通过一根轻弹簧与另一个相同的小球B相连.A,B静止不动时,弹簧伸长3.0cm.今将细线烧断,A,B便与弹簧一起下落,假设B触及地面上的橡皮泥时,弹簧的伸长量正好也是3.0cm,而后B与橡皮泥发生完全非弹性碰撞.考虑到A将会继续朝下运动,试求而后弹簧相对其自由长度的最大压缩量.
1700988530
1700988531

1700988532
1700988533
1700988534
图 7-112(题7-51)
1700988535
1700988536
7-52 在光滑的水平桌面上开有一小孔,一根穿过小孔的细绳两端各系一质量分别为m1和m2的小球,位于桌面上的小球m1以v0的速度绕小孔作匀速圆周运动,桌面下小球m2则悬在空中,保持静止.
1700988537
1700988538
(1)求位于桌面部分的细绳的长度l0;
1700988539
1700988540
(2)若给m1一个径向的小冲量,则m2将作上下振动,求振动角频率ω.
1700988541
1700988542
7-53 在天花板下用两根长度同为l的轻绳悬挂一质量为M的光滑匀质平板,板的中央有一质量为m的光滑小球.开始时系统处于静止的水平状态,而后如图7-113所示,使板有一水平方向的小初速度v0,此板便会作小角度摆动.假设摆动过程中细绳始终处于伸直状态,试求板的摆动周期.