1700988843
1700988844


1700988845
1700988846
1700988847
直尺相对S系是运动的,S系中测量运动直尺长度的一个可取方案是在同一时刻测定动点A′,B′在x轴上的坐标,这两个坐标量之间的差值即为直尺的运动长度.例如在S系计时系统中如图8-6所示,测得A′在t1=1:00时刻位于x1,B′在t2=1:00时刻位于x2,便有
1700988848
1700988849


1700988850
1700988851
1700988852


1700988853
1700988854
1700988855
图 8-6
1700988856
1700988857
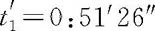
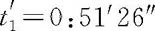
1700988858


1700988859
据前所述,S′系按自己的计时系统认定x1,x2两处时钟零点校准有差异,x1处时钟拨快了(t1=1:00对应S′系计时系统),x2处时钟拨慢了(t2=1:00对应S′系计时系统).S′系认为因相对运动这种先测头部A′位置,后测尾部B′位置的必然结果是
1700988860
1700988861


1700988862
1700988863
1700988864
这就是运动直尺的长度收缩.l静即为S′系中两个静止点之间的空间间距度量值,l动则是S系中这两个运动点之间的空间间距度量值,l动≠l静正是惯性系之间空间间距度量相对性的表现.
1700988865
1700988866
(3)运动时钟计时率的变慢(时间间隔度量的相对性)
1700988867
1700988868
在(2)中给出了S系测量运动直尺长度的一个方案,且据(1)导得l动<l静.
1700988869
1700988870
S系测量运动直尺长度的第二个可取方案是测出直尺A′B′通过x轴上某一静止时钟P所经历的时间间隔t2-t1,则有
1700988871
1700988872


1700988873
1700988874
1700988875


1700988876


1700988877


1700988878
其中t1,t2分别是A′,B′与P相遇时P的读数.若如图8-7所示,S′系中在A′,B′放置两个静止时钟,A′与P相遇时A′时钟读数记为,B′与P相遇时B′时钟读数记为.那么S′系认为随S系一起相对S′系运动的时钟P,在时间间隔内通过的路程即为直尺A′B′的静止长度,便有
1700988879
1700988880


1700988881
1700988882
1700988883


1700988884
1700988885
1700988886
图 8-7
1700988887
1700988888
因l动<l静,即得
1700988889
1700988890


1700988891
1700988892