1700989518


1700989519
1700989520
1700989521
在S″系中替身从星球P到达地球,经时
1700989522
1700989523


1700989524
1700989525
1700989526
故替身左手时钟读数为
1700989527
1700989528


1700989529
1700989530
1700989531
可见,确有
1700989532
1700989533
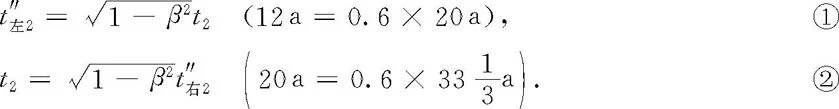
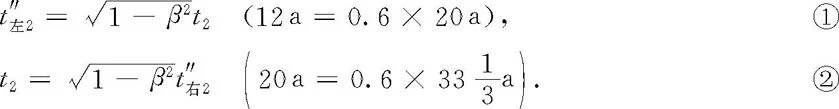
1700989534
1700989535
1700989536
第①式表明,若将哥哥的前半段经历(从地球到星球P)和替身的后半段经历(从星球P到地球)组合成半真半假的“哥哥”经历,那么“兄”弟见面时,确实是“哥哥”比弟弟年轻.但这样的“哥哥”不是双生子佯谬中真实的哥哥,故上述解答不能替代双生子佯谬的真实解答.
1700989537
1700989538


1700989539


1700989540
第②式表明,S″系中O″处和处的两个静止时钟测得的从哥哥离开弟弟,到替身见到弟弟的过程经历的时间间隔与弟弟手中相对S″系运动的一个时钟测得的时间间隔t2之间的关系,仍然与运动时钟计时率变慢公式相符.
1700989541
1700989542
例10 关于隧道问题.
1700989543
1700989544
已知隧道A1B1的长度为L1,火车A2B2的静长为L2>L1.
1700989545
1700989546
(1)如图8-18所示,设火车以匀速度v驶进隧道,使得地面系S1中的观察者发现A2与A1相遇时,B2与B1也相遇,试求v值.
1700989547
1700989548


1700989549
1700989550
1700989551
图 8-18
1700989552
1700989553
(2)引入随火车一起运动的惯性系S2,在S2系中的观察者必定认为A1与A2先相遇,而后B1与B2相遇,试求其间的时间间隔∆t2.
1700989554
1700989555
(3)设隧道A1端封闭,B1端有一大门.S1系中的观察者既然认定A2与A1相遇时B2与B1也相遇,便可在这一时刻把B1端的大门关闭,将火车A2B2装入隧道.设S2系不会因火车运动受阻而减速,即S2始终是一个惯性系.S2系的观察者认为A1与A2相遇后,需经∆t2时间,B1才与B2相遇,但又必须承认火车会被装入隧道这一事实.为此,S2系的观察者提出一种可能的物理模型来进行解释.
1700989556
1700989557
为简化,设隧道A1封闭端足够结实,形变可略,当A1封闭端与火车的A2端相遇时,即会带动A2端以v速度朝着图8-19的右方运动.如果A2被带动的瞬间,火车的所有部位(包括B2端)都被以v速率朝右带动,即若火车具有经典的刚性结构,则隧道不可能将火车关入.现在假设被带动事件在火车中以一恒定的有限速度u从A2端传递到B2端,便有可能在B2端被带动之前或被带动之时,B1已到达B2位置,则B1端的大门可将火车关入.
1700989558
1700989559


1700989560
1700989561
1700989562
图 8-19
1700989563
1700989564
试先根据上述模型,确定u的可取值,再假设u是一个独立于v和L2的火车内部结构参量,试证明u≤c.
1700989565
1700989566
(本题意在使读者了解到狭义相对论中相互作用变化传递速度的有限性.)
1700989567