1700990076
1700990077
质点1:u1=0,F1=F1yj;
1700990078
1700990079
质点2:u2=ui,F2=F2yj;
1700990080
1700990081
F2y=-F1y ⇒ F1+F2=0.
1700990082
1700990083
S′系:
1700990084
1700990085
质点1:
1700990086
1700990087


1700990088
1700990089
1700990090
质点2:
1700990091
1700990092
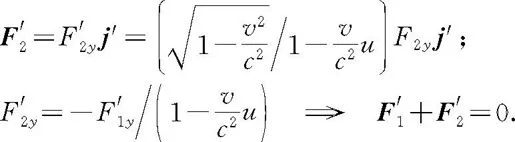
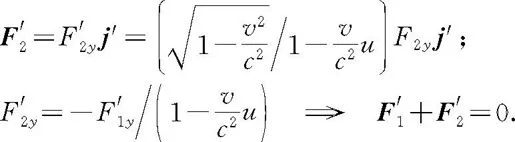
1700990093
1700990094
1700990095
狭义相对论中牛顿第三定律虽然不能成立,但在狭义相对论之前已经建立的普遍的动量守恒定律(即任何一个与外界无相互作用的系统,其动量守恒)仍然成立.
1700990096
1700990097
二、动量及能量变换
1700990098
1700990099
据(8.27)式,可得质点动量定理:
1700990100
1700990101


1700990102
1700990103
1700990104
质点动量定理与牛顿第二定律原始形式完全等价,两者的惯性系不变性一致,只需讨论(8.28)式的惯性系不变性即可.
1700990105
1700990106
继承经典力学中的质点动能定理,狭义相对论中可将与质点运动状态有关的能量记为E,假设力F对质点所作功仍然等于E的增量,即有
1700990107
1700990108


1700990109
1700990110
1700990111
假设(8.28)和(8.29)都是惯性系不变式,则有
1700990112
1700990113


1700990114
1700990115
1700990116
将dx=uxdt,udt=dl代入后,可得
1700990117
1700990118


1700990119
1700990120
1700990121
积分后可得
1700990122
1700990123


1700990124
1700990125