1700990318
1700990319
相互对比,可见取C1=0和C2=0是自洽的.
1700990320
1700990321
例18 狭义相对论动质量公式和质能关系式的微积分导出.
1700990322
1700990323
(1)设牛顿第二定律的原始形式具有惯性系不变性,即有
1700990324
1700990325


1700990326
1700990327
1700990328
再设同一质点在任一惯性系中的静质量同为m0.试由x方向力、加速度变换式
1700990329
1700990330


1700990331
1700990332
1700990333
(后一变换式参见本章例15)导出质点动质量公式
1700990334
1700990335


1700990336
1700990337
1700990338
(2)在狭义相对论中,假设质点动能定理
1700990339
1700990340


1700990341
1700990342
1700990343
仍然成立,试由质点动质量公式导出质点的质能关系式
1700990344
1700990345


1700990346
1700990347
1700990348
解 (1)设质点仅沿x′,x方向运动,且仅沿x′,x方向受力,则有
1700990349
1700990350


1700990351
1700990352
1700990353


1700990354
1700990355
1700990356
设S′系为质点的瞬时静止惯性系,则有
1700990357
1700990358


1700990359
1700990360
1700990361


1700990362
代入Fx表达式,可得
1700990363
1700990364
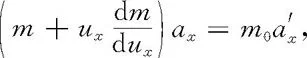
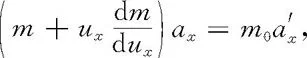
1700990365
1700990366
1700990367

