1700990351
1700990352
1700990353


1700990354
1700990355
1700990356
设S′系为质点的瞬时静止惯性系,则有
1700990357
1700990358


1700990359
1700990360
1700990361


1700990362
代入Fx表达式,可得
1700990363
1700990364
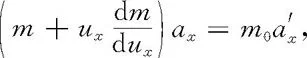
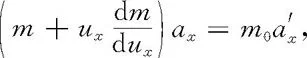
1700990365
1700990366
1700990367


1700990368
将关系式代入后,又可得
1700990369
1700990370


1700990371
1700990372
1700990373
S′系相对S系的速度v=ux,将ux省记为u,则有
1700990374
1700990375


1700990376
1700990377
1700990378
此式可解释为:质点在S系中沿x方向运动速度为u时,对应的质量为m,则m,u间有上述关联.
1700990379
1700990380
将上式改述成一阶微分方程
1700990381
1700990382


1700990383
1700990384
1700990385


1700990386
可得通解 A为积分常量.
1700990387
1700990388


1700990389
将代入后,又可得
1700990390
1700990391


1700990392
1700990393
1700990394
因u→0时,m→m0,故积分常量A=0,即得动质量公式
1700990395
1700990396


1700990397
1700990398
1700990399
(2)由F=d(mu)/dt,可得
1700990400