1700991001
(2)火箭出发时的静止质量M0和到达目的地时的静止质量之间的比值.
1700991002
1700991003
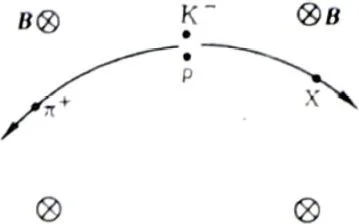
8-46 如图8-48所示,在一次粒子碰撞实验中,观察到一个低速K-介子与一个静止质子p发生相互作用,生成一个π+介子和一个未知的X粒子,在匀强磁场B中π+介子和X粒子的轨迹已在图中画出.已知B=1.70T,测得π+介子轨迹的曲率半径为R1=34.0cm.
1700991004
1700991005

1700991006
1700991007
1700991008
图 8-48(题8-46)
1700991009
1700991010
(1)试确定X粒子轨迹的曲率半径R2;
1700991011
1700991012
(2)试参考下表确认X为何种粒子.
1700991013
1700991014


1700991015
1700991016
1700991017
8-47 μ-子的电量q=-e(e=1.6×10-19C),静质量m0=100MeV/c2,静止时的寿命τ0=10-6s.设在地球赤道上空距地面高度h=104m处有一个μ-子以接近于真空光速的速度垂直向下运动.
1700991018
1700991019
(1)试问此μ-子至少应有多大的总能量才可到达地面?
1700991020
1700991021
(2)若把赤道上空104m高度范围内的地球磁场处理成水平匀强磁场,B=10-4T,试求上述已获得能量的μ-子在到达地面时的偏离方向和总的偏转角.
1700991022
1700991023
8-48 某粒子的静止质量为m0,以初速v0从t=0开始沿x轴方向运动,运动期间始终受到一个指向y轴方向的恒力F的作用.试证,任意t>0时刻粒子的两个速度分量为
1700991024
1700991025


1700991026
1700991027
1700991028
进而证明,当t→∞时,速率v→c,vx→0.
1700991029
1700991030
8-49 在惯性系某个S平面上的O点有一个带电量为Q>0的固定点电荷,另一个带负电荷-q的质点P受点电荷Q的库仑力作用,绕O点在S平面上作有界曲线运动.设P点的初始相对论能量为E0,P点相对O点的初始角动量为L0,且有
1700991031
1700991032
qQ/4πε0L0c≪1,
1700991033
1700991034
其中c为真空光速.
1700991035
1700991036
(1)试证在零级近似下,即在qQ/4πε0L0c≈0的条件下,P点的运动轨道是一个椭圆;
1700991037
1700991038
(2)试证P点的真实运动是带有进动的椭圆运动,并求出P点相对O点的径矢长每变化一周对应的进动角∆θ.
1700991039
1700991040
8-50 引力红移和恒星质量的测定
1700991041
1700991042
(1)频率为ν的一个光子具有惯性质量,此质量由光子的能量确定.在此假定下,光子也有引力质量,量值等于惯性质量.与此相应,从一颗星球表面向外发射出的光子,逃离星球引力场时,便会损失能量.
1700991043
1700991044
试证明,初始频率为ν的光子从星球表面到达无穷远处,若将它的频移(频率增加量)记为∆ν,则当|∆ν|≪ν时,有
1700991045
1700991046


1700991047
1700991048
1700991049
式中M为星球质量,R为星球半径.这样,在距星球足够远处对某条已知谱线频率红移的测量,可用来测出比值M/R,如果知道了R,星球的质量M便可确定.
1700991050