1700991326
参照图B-5,引入B沿A方向的投影B∥,或A沿B方向的投影A∥,即有
1700991327
1700991328


1700991329
1700991330
1700991331
则有
1700991332
1700991333


1700991334
1700991335
1700991336


1700991337
其中B∥,A∥均可正,可负,也可为零.图B-5所示,取成锐角,B∥,A∥都为正.
1700991338
1700991339


1700991340
1700991341
1700991342
图 B-5
1700991343
1700991344
通过标积,可将A的模量和分量各自表述成
1700991345
1700991346
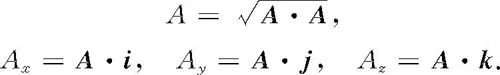
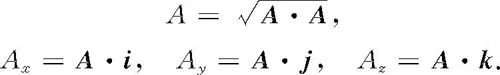
1700991347
1700991348
1700991349
由标积的定义式,不难导出它的一些基本性质,如
1700991350
1700991351


1700991352
1700991353
1700991354
进一步可以导出其他公式,例如:
1700991355
1700991356


1700991357
1700991358
1700991359
3维空间中有
1700991360
1700991361


1700991362
1700991363
1700991364
借此可导出标积的表达式
1700991365
1700991366


1700991367
1700991368
1700991369
k维空间中有
1700991370
1700991371


1700991372
1700991373
1700991374
δij称为克罗内克尔符号.两个k维空间矢量A,B的标积可表述成
1700991375