1700995472


1700995473
数学界把这类计数问题称作“组合”(combinations),把这种形式的数字称作“二项式系数”(binomial coefficients),把需要考虑先后次序的计数问题称作“排列”(permutations)。这些术语在使用时很容易发生混淆,例如,我们经常把“密码锁”说成“combination lock”(数字组合锁),实际上应该是“permutation lock”(数字排列锁),因为数字的先后次序非常重要。
1700995474
1700995475
如果冰激凌店出售20种口味的冰激凌,你希望在一个圆筒中装5种不同口味的冰激凌(次序不重要),那么各种组合的数量为:
1700995476
1700995477


1700995478
1700995479
1700995480


1700995481
顺便告诉大家,如果你们的计算器没有专门计算的按钮,也可以使用互联网,在搜索引擎中输入“20选5”,就可能会找到答案。
1700995482
1700995483


1700995484


1700995485


1700995486
二项式系数有时会出现在似乎需要考虑先后次序的问题之中。如果我们抛10次硬币,硬币正反面的排列方式(例如,正反正反反正正反反反,正正正正正正正正正正)有多少种呢?由于每次抛掷都有两个可能的结果,因此根据乘法法则,一共有210= 1 024个可能的排列,而且每种结果的发生概率都是相同的。(第一次听到这个结论时,有些人会感到吃惊,因为他们认为得到例子中给出的第二种结果的概率小于第一个。但实际上,得到这两个结果的概率都是。)不过,抛10次硬币,得到4个正面的概率大于10个正面,这是因为只有一种情况可以得到10个正面,这种情况发生的概率是。那么,抛10次得到4个正面的情况有多少种呢?这样的排列要求10次中有4次是正面朝上,其他6次都是反面朝上。从10次中选取4次,共有= 210种排列方式。(与从10种口味中选择4种不同口味冰激凌的情况相似。)因此,抛掷10次硬币,在公平公正的情况下,正好得到4个正面的概率是:
1700995487
1700995488
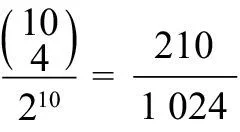
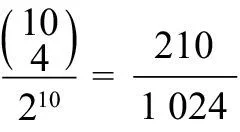
1700995489
≈20%
1700995490
1700995491
延伸阅读
1700995492
1700995493


1700995494


1700995495


1700995496
我们自然而然地就会想到一个问题:从10种口味的冰激凌中挖3个球,可以重复选择同一口味,一共可以制成多少种圆筒冰激凌?(103/ 6显然不是正确答案,因为它连整数都不是!)直接的解法是:根据每个圆筒中有几种口味的冰激凌,分三种情况考虑。如果只有1种口味,自然只有10种可能。如果有3种口味,根据前面的讨论,我们知道共有= 120种可能。如果有2种口味,我们知道有种选取办法,然后还要考虑哪种口味挖2个球,因此共有2×= 90种可能。把这三种情况汇总起来,共可以制作出10 + 120 + 90 = 220种圆筒冰激凌。
1700995497
1700995498
还有一种解法,无须分成三种情况,也可以得到正确答案。所有的圆筒冰激凌都可以表示成3个星号和9条竖线的形式。例如,选择第1、2、2种口味的冰激凌可以表示成下面这种星号—竖线排列:
1700995499
1700995500


1700995501
1700995502
1700995503
选择第2、2、7种口味时,上述排列就会变成:
1700995504
1700995505


1700995506
1700995507
1700995508
下面这种排列
1700995509
1700995510


1700995511
1700995512
1700995513


1700995514


1700995515
则表示圆筒中有第3、5、10种口味的冰激凌。3个星号与9条竖线的所有排列均对应不同的圆筒冰激凌。这些符号一共占据12个位置,其中3个位置上是星号。因此,星号与竖线的排列一共有= 220种。推而广之,从n个对象中选取k个对象,不考虑先后次序,而且可以重复选取,可选方案的数量就是k个星号与n– 1条竖线构成的排列,也就是说,有种选择方案。
1700995516
1700995517


1700995518
1700995519
1700995520


1700995521
很多涉及概率问题的游戏都与组合有关。例如,在购买如上图所示的加州彩票时,你需要从1~47中选择5个不同的号码,此外,还需要在1~27中选择一个MEGA号码(该号码也可以是你选择的另外5个号码中的一个)。因此,MEGA号码共有27种选择,另外5个号码共有种选择。那么,加州彩票的号码组合共有: