1701042750
1701042751
图3-2
1701042752
1701042753
从直观上看,Möbius带与平环有许多不同之处.首先,平环的边界是两条封闭曲线,它们分别由原矩形的上下边将两端点粘合而得到;而制造Möbius带时,原矩形上边的两端与下边两端粘合,连成一条曲线,因此Möbius带的边界是一条封闭曲线.其次,平环是双侧的,Möbius带是单侧的.当然,局面地看,Möbius带上每一点附近的面块有两个侧向,但从整体上看,这两侧是连成一片的,从某一点的一侧在带上移动可以到达该点的另一侧,中间不用翻越边界.在平环上这是做不到的.还有,沿平环的中线割开可将平环分割成两个平环,而沿Möbius带的中线割开得到的还是连通的一条带子(请读者说明这是一个平环).以上的差别,从直观上说明了平环与Möbius带不同胚.以后会严格证明它们是不同胚的.
1701042754
1701042755
1.2 环面和Klein瓶
1701042756
1701042757
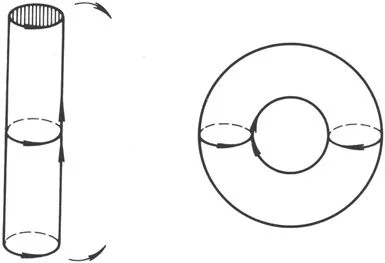
环面和Klein瓶都可以用一截圆柱面(平环)将两个截口互相粘接而得到.
1701042758
1701042759

1701042760
1701042761
1701042762
图3-3
1701042763
1701042764
如果每一直母线段的两端粘合,所得到的是环面(图3-3),两个截口是以相同的方向相粘接的.如果让两个截口方向相反地粘接,则得到Klein瓶(图3-4).要实现这样的粘接,必须将圆柱面弯曲后,把一端穿过管壁进入管内与另一端相接.在3维空间中这是做不到的,因为在进入管内之处必然要相交.但在4维空间中可以实现(让相交点的第四个坐标不同,从而把它们分开).
1701042765
1701042766


1701042767
1701042768
1701042769
图3-4
1701042770
1701042771
Klein瓶也是单侧的(图3-4),以后要证明它与环面不同胚.
1701042772
1701042773
环面是一种常见曲面.各种轮胎的表面是环面;圆周绕着与它共面但相离的轴线旋转得到环面(图3-5),称此圆周上的点旋出的圆为纬圆,以轴线为界的半平面与环面的交线称为经圆;S1×S1是环面(§2习题6).一般地记Tn=S1×…×S1,称为n维环面.这里讨论的是2维环面T2.
1701042774
1701042775


1701042776
1701042777
1701042778
图3-5
1701042779
1701042780
和平环一样,环面和其他曲面都是一个拓扑等价类中空间的统称.
1701042781
1701042782
1.3 射影平面
1701042783
1701042784
射影平面记作P2,它是射影几何学中的概念.拓扑学中,有几种描述它的方法,其中之一是把圆盘D2(它同胚于矩形面块)的边界S1上每一对对径点(同一直径的两个端点)粘合,得到射影平面(图3-6).这种粘接直观上就不好理解了,在3维欧氏空间中是做不到的,在4维空间中能实现,但也不好想象.我们将在后面说清楚它.
1701042785
1701042786


1701042787
1701042788
1701042789
图3-6
1701042790
1701042791
用“粘合”方法制造新拓扑空间是拓扑学中常用的一种方法.还有许多更复杂的“粘合”,凭直观是不好接受的.例如,把圆盘D2与I的乘积空间D2×I的一端(子集D2×{1})捏为一点,得到的空间的直观形象是一个圆锥体(图3-7).如果用一般拓扑空间X代替D2,得到的空间是什么?又如把环面上的一个经圆和一个纬圆捏在一起成一个点,又会得到什么空间?这些问题都不能靠直观来回答.
1701042792
1701042793


1701042794
1701042795
1701042796
图3-7
1701042797
1701042798
从拓扑学的观点来说,需要有一种描述粘合所得到的新空间(不论它在直观上能否接受)的拓扑的方法.这就是下一节要解决的问题.
1701042799