1701043869
例如D2,I以及欧氏空间的任何凸集都是单连通的.
1701043870
1701043871
命题4.10 设A是X的一个道路分支,x0∈A,i:A→X是包含映射.则
1701043872
1701043873
iπ:π1(A,x0)→π1(X,x0)
1701043874
1701043875
是同构.
1701043876
1701043877
证明 设a是X上在x0处的闭路.a(I)是道路连通的,并且包含x0,因此a(I)⊂A.这样a也可看作A中的道路,由此得出iπ是满的.
1701043878
1701043879


1701043880


1701043881
如果在X中,则H的像也是包含x0的道路连通子集,从而在A中.这说明在A中也有由此得到iπ是单的. ▎
1701043882
1701043883
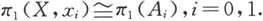
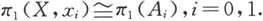
1701043884
设x0,x1在X的不同的道路分支中.记Ai是包含xi的道路分支,命题说明
1701043885
1701043886
一般来说,π1(A0)与π1(A1)是没有什么联系的.因此当x0,x1不在同一道路分支中时,π1(X,x0)与π1(X,x1)没有关系.
1701043887
1701043888
习 题
1701043889
1701043890
1.设X是平凡拓扑空间.证明对任何x0∈X,π1(X,x0)是平凡群.
1701043891
1701043892
2.设X是离散拓扑空间,x0∈X.证明π1(X,x0)是平凡群.
1701043893
1701043894
3.设x0是(R,τ2)(见第二章§6)的一点,证明(R,τ2)在x0的基本群是平凡群.
1701043895
1701043896
4.设f:X→Y连续,xi∈X,yi=f(xi),i=0,1.记ω是从x0到x1的道路类.证明下面的同态图表可交换:
1701043897
1701043898


1701043899
1701043900
1701043901
5.设A是X的收缩核,i:A→X是包含映射,r:x→A是收缩映射.证明∀x0∈A,iπ:π1(A,x0)→π1(X,x0)是单同态,rπ:π1(X,x0)→π1(A,x0)是满同态.
1701043902
1701043903


1701043904


1701043905
6.设X单连通,a,b是X中有相同起、终点的道路,证明
1701043906
1701043907


1701043908


1701043909


1701043910
7.设ω#,是x0到x1的两个道路类.证明在π1(X,x0)的中心里(即ωω′-1与任一α∈π1(X,x0)都可交换:ωω′-1α=αωω′-1).
1701043911
1701043912


1701043913
8.证明若x0,x1在X的同一道路分支中,则从x0到x1的任一道路类决定相同的同构π1(X,x0)是交换群.
1701043914
1701043915
9.试直接构造从(ab)c到a(bc)的定端同伦.
1701043916
1701043917
基础拓扑学讲义 [:1701040219]
1701043918
§3 Sn的基本群