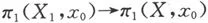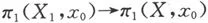1701044505
1701044506
(1)球面S2加一条直径(图4-25(a));
1701044507
1701044508
(2)在环面的一个纬圆上粘接一个圆盘(图4-25(b));
1701044509
1701044510
(3)球面S2加一圆周S1(它们相切,图4-25(c)).
1701044511
1701044512


1701044513
1701044514
1701044515
图4-25
1701044516
1701044517


1701044518
14.证明
1701044519
1701044520


1701044521
15.证明
1701044522
1701044523
16.设ι是E3中一条直线.证明π1(E3ι)是自由循环群.
1701044524
1701044525
基础拓扑学讲义 [:1701040221]
1701044526
§5 基本群的计算与应用
1701044527
1701044528
同伦不变性是计算基本群的有效工具.本节介绍计算基本群的另一个常用工具:Van-Kampen定理,它也能把复杂空间基本群的计算转化为较简单空间基本群的计算.本节还将介绍基本群的几个有代表性的应用.
1701044529
1701044530
5.1 Van-Kampen定理
1701044531
1701044532
Van-Kampen定理的叙述和证明都比较复杂,并涉及到较多的代数概念.许多文献中用母元与关系这种表示群的语言来叙述这个定理.本书中采用一种较容易接受的形式来表述.将要用到两个群的自由乘积的概念,读者可以在附录A中找到它的定义.定理的证明也不放在正文中,列为本书的附录B.附录B中还写出了用母元与关系这种语言来叙述Van-Kampen定理的方式.
1701044533
1701044534
k个自由循环群的自由乘积②称作秩为k的有限生成自由群.在每个自由循环群中取定生成元,得元素组{a1,a2,…,ak},则该有限生成自由群的每个元素都可唯一地用这组元素表出,因此把它称为由{a1,…,ak}自由生成的自由群,并记作F(a1,a2,…,ak).
1701044535
1701044536
易证F(a1,…,ak)*F(b1,…,bι)=F(a1,…,ak,b1,…,bι).
1701044537
1701044538
设A是群G的子集,把G中包含A的最小的子群称为由A生成的子群,记作〈A〉;把G中包含A的最小正规子群称为由A生成的正规子群,记作[A].
1701044539
1701044540
现在叙述定理.
1701044541
1701044542
定理4.7(Van-Kampen定理) 如果拓扑空间X可分解为两个开集X1与X2之并,并且X0=X1∩X2非空,道路连通.则∀x0∈X0,有
1701044543
1701044544
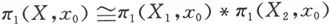
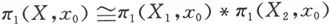
1701044545
1701044546
1701044547


1701044548
1701044549
1701044550
其中iι:X0→Xι(ι=1,2)是包含映射.
1701044551
1701044552


1701044553
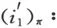
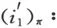
1701044554