打字猴:1.701044538e+09

1701044538 设A是群G的子集，把G中包含A的最小的子群称为由A生成的子群，记作〈A〉；把G中包含A的最小正规子群称为由A生成的正规子群，记作［A］．

1701044539

1701044540 现在叙述定理．

1701044541

1701044542 定理4.7（Van-Kampen定理）　如果拓扑空间X可分解为两个开集X1与X2之并，并且X0＝X1∩X2非空，道路连通．则∀x0∈X0，有

1701044543

1701044544

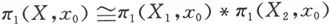
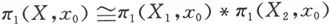
1701044545

1701044546

1701044547

1701044548

1701044549

1701044550 其中iι：X0→Xι（ι＝1，2）是包含映射．

1701044551

1701044552

1701044553

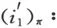
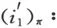
1701044554

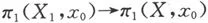
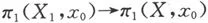
1701044555

1701044556 如果记也是包含映射，则同态和决定唯一的同态φ：π1（X1，x0）*π1（X2，x0）→π1（X，x0）（习题1）．定理的结论可以明确地表述成：φ是满同态，并且Kerφ＝［｛（i1）π（α）（i2）π（α-1）｜α∈π1（X0，x0）｝］．这就给出了定理要证明的两个方面，其中φ是满同态的证明还不算太困难（习题2），麻烦的是另一部分．有兴趣的读者可以参看附录B，也可在参考书目［4］和［5］中找到证明．

1701044557

1701044558 定理要求X1，X2都是开集，在许多情况下显得不方便．下面给出它的替代形式．

1701044559

1701044560 定理4.7a　如果定理4.7中X1，X2都改为闭集，并且X0是它的一个开邻域的强形变收缩核，其他条件不变，则结论仍成立．

1701044561

1701044562 对于不大熟悉代数的人，Van-Kampen定理的结论不大好理解，也不好应用．好在在本书中只在下列两种特殊的情形应用定理，对代数知识的依赖要少得多．

1701044563

1701044564 （1）X0是单连通的，这时结论简化为

1701044565

1701044566