1701047518
f*q=(h0)*q=(h1)*q=g*q, ∀q∈Z. ▎
1701047519
1701047520
命题7.12 设K和L是复形,f∶|K|→|L|是一个同伦等价,则f*q∶Hq(K)→Hq(L)是同构,∀q∈Z.
1701047521
1701047522
证明 设g∶|L|→|K|是f的同伦逆,则
1701047523
1701047524


1701047525


1701047526
g*qf*q=(gf)*q=id*q∶Hq(K)→Hq(K),
1701047527
1701047528


1701047529


1701047530
f*qg*q=(fg)*q=id*q∶Hq(L)→Hq(L),
1701047531
1701047532
因此f*q是同构,g*q=(f*q)-1. ▎
1701047533
1701047534
一个直接的推论是定理7.6.
1701047535
1701047536


1701047537
定理7.6 设K和L是复形,若则
1701047538
1701047539


1701047540
q∈Z. ▎
1701047541
1701047542
4.2 同伦不变性在同调群的计算中的应用
1701047543
1701047544
同伦不变性是计算同调群的有效工具,它常常可在很大程度上简化计算.例如,不难看出单纯锥的多面体是可缩空间,而显然由一个0维单形构成的多面体是零调的,即0维同调群是自由循环群,其他维同调群是零群.用同伦不变性立即推出单纯锥也是零调的(但第六章的计算还是必要的,在定义f*q的过程中要用到这个结果).又如,平环与S1同伦等价,因此它的同调群与S1的同调群(即2维单形的边缘复形的同调群)同构.(对照第六章§4的例2与例3的结果.)下面再举几个例子.
1701047545
1701047546
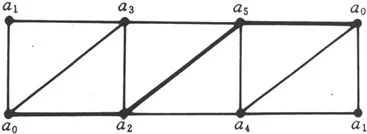
例1 Möbius带X的同调群.
1701047547
1701047548

1701047549
1701047550
1701047551
图7-10
1701047552
1701047553


1701047554
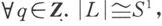
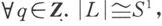
1701047555
图7-10是X的一个剖分K的展开图.设L={(a0,a2),(a2,a5),(a5,a0);a0,a2,a5},它是K的子复形,并且|L|是|K|的形变收缩核.记i∶|L|→|K|是包含映射,则因此有
1701047556
1701047557


1701047558
1701047559
1701047560
并且,设z=a0a2+a2a5+a5a0,则z是Z1(L)=H1(L)的生成元,因而〈z〉是H1(K)的生成元.
1701047561
1701047562
例2 Klein瓶的同调群.
1701047563
1701047564
图7-11是Klein瓶的一个剖分K的展开图.
1701047565
1701047566


1701047567