1701048330


1701048331
令,则A为所求. ▎
1701048332
1701048333
定理A.1 没有有限阶非0元素的有限生成交换群是自由群.
1701048334
1701048335


1701048336
证明 设H是有限生成交换群.它没有有限阶非0元素.假设H的生成元组包含元素个数的最小值为n,并且{a1,a2,…,an}是一个生成元组.用反证法说明{a1,a2,…,an}自由生成H.否则,有不全为0的整数r1,r2,…,rn,使得r1a1+r2a2+…+rnan=0.由于H没有有限阶非0元素,不妨可设最大公约数(r1,r2,…,rn)=1.由引理,存在使得
1701048337
1701048338


1701048339
1701048340
1701048341
令(b1,b2,…,bn)=(a1,a2,…,an)A-1,则{bi}也是H的生成元组,并且
1701048342
1701048343


1701048344
1701048345
1701048346
于是{b2,…,bn}也是H的生成元组,它只有n-1个元素.与假设矛盾. ▎
1701048347
1701048348
推论 设H0是有限生成交换群H的子群,则H/C(H0)是自由交换群.特别地,H/TH是自由交换群. ▎
1701048349
1701048350
2.直和
1701048351
1701048352


1701048353
交换群的直和就是普通群的直积概念.两个交换群H1和H2的直和是一个交换群,记作H1H2,其集合为
1701048354
1701048355
{(h1,h2)|hi∈Hi,i=1,2}.
1701048356
1701048357
加法由
1701048358
1701048359


1701048360
1701048361
1701048362
规定.
1701048363
1701048364
任意有限个交换群的直和可类似地规定.
1701048365
1701048366


1701048367


1701048368


1701048369


1701048370
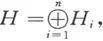
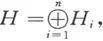
1701048371
设H有一组子群H1,H2,…,Hn,使得∀h∈H可唯一地表示为则(容易验证,给出到H的同构).在这种情况,称H是H1,H2,…,Hn的内直和(经常简单地称为直和),记作称Hi是H的直和因子(也称作直加项).
1701048372
1701048373
设F是有限基自由交换群,{f1,f2,…,fn}是它的基,记〈fi〉是fi生成的自由循环群,则
1701048374
1701048375


1701048376
1701048377
1701048378


1701048379
命题A.3 设H1,H2是H的子群,H1+H2=H(即∀h∈H,有表示式h=h1+h2,hi∈Hi),并且H1∩H2=0,则H=H1H2.