1702638845
1702638846
例1 大学生酗酒问题
1702638847
1702638848


1702638849
高风险行为在人群中有多普遍?“行为风险因素监测系统”(BRFSS)是全球最大的以电话访问的形式进行持续健康调查的机构,早在1984年它就开始逐年跟踪美国人的健康状况和高风险行为。该调查结果可以在美国疾病控制和预防中心网站上看到。这个调查每个月都会从美国50个州、哥伦比亚特区、波多黎各、美属维京群岛和关岛收集数据。在加利福尼亚州,2010年BRFSS访问了一个包含6911名大学生的简单随机样本,其中有792人说他们那一年有过酗酒经历。酗酒是指男性一次喝5个或以上标准饮酒量的酒,女性一次饮用4个或以上标准饮酒量的酒。这个结果可能因为有些人不愿意如实告知酒精摄入量而出现偏差(见练习21.14),而在这里,我们假设调查对象说的都是真话。基于这些数据,我们如何判断2010年加州全体大学生中有多少百分比的人酗酒?我们把这个未知的参数p称为“比例”,用于估算参数p的是样本统计量。
1702638850
1702638851


1702638852
1702638853
1702638854
统计推断的一个基本步骤,就是用样本统计量来估计总体参数。一旦我们取得样本,就可以估算出所有加州大学生中2010年有过酗酒经历的人的比例“大约为11.5%”,因为样本统计量是11.5%。我们只能估计总体参数“大约”是这个数字,因为我们知道样本结果通常不会和总体的真实结果一模一样。置信区间把这个“大约”精确化了。
1702638855
1702638856
95%置信区间
1702638857
1702638858
95%置信区间是根据样本数据计算出来的一个区间,保证在所有样本当中,有95%的样本统计量会包含在该区间之中。
1702638859
1702638860
我们会先介绍总体参数的置信区间,再讨论我们实际上做了什么,并且稍加推广。
1702638861
1702638862
95%置信区间
1702638863
1702638864


1702638865


1702638866


1702638867
我们要估计总体成员中拥有某种特征的比例p,这个特征可能是他们有工作,或者他们对总统的表现满意等。让我们把正在考虑的这个特征叫作“成功”。我们会用简单随机样本的成功比例,来估计总体的成功比例p。样本统计量作为总体参数p的估计值,表现如何?想要得到答案,我们应该问:“如果我们取许多个样本,会发生什么情况?”我们知道,的值会随样本而变,我们也知道这个变异性不是偶发的。长期下来,它有很清楚的形态,用正态曲线可以把这个形态比较准确地描绘出来。
1702638868
1702638869
样本统计量的抽样分布
1702638870
1702638871


1702638872
样本统计量的抽样分布,是指从同一总体中抽出的同样大小的所有可能样本,其统计量之值的分布。从一个成功比例为p的很大的总体中抽取一个大小为n的简单随机样本,用表示成功的样本统计量:
1702638873
1702638874


1702638875
1702638876
1702638877
当样本够大时,
1702638878
1702638879


1702638880
•的分布接近于正态分布。
1702638881
1702638882
• 抽样分布的平均数和p相等。
1702638883
1702638884
• 抽样分布的标准差是:
1702638885
1702638886
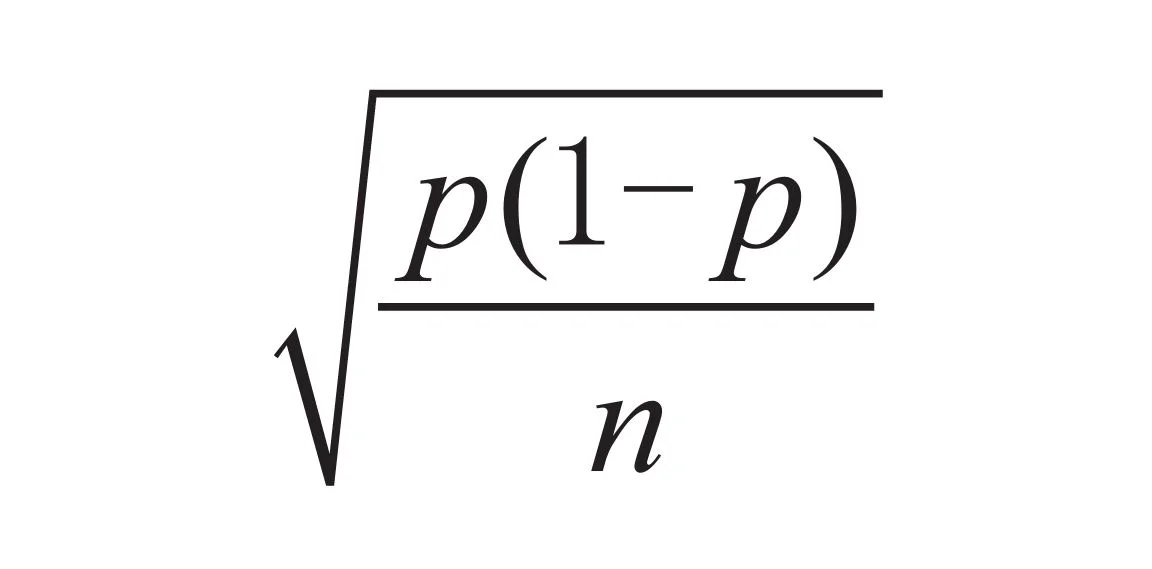
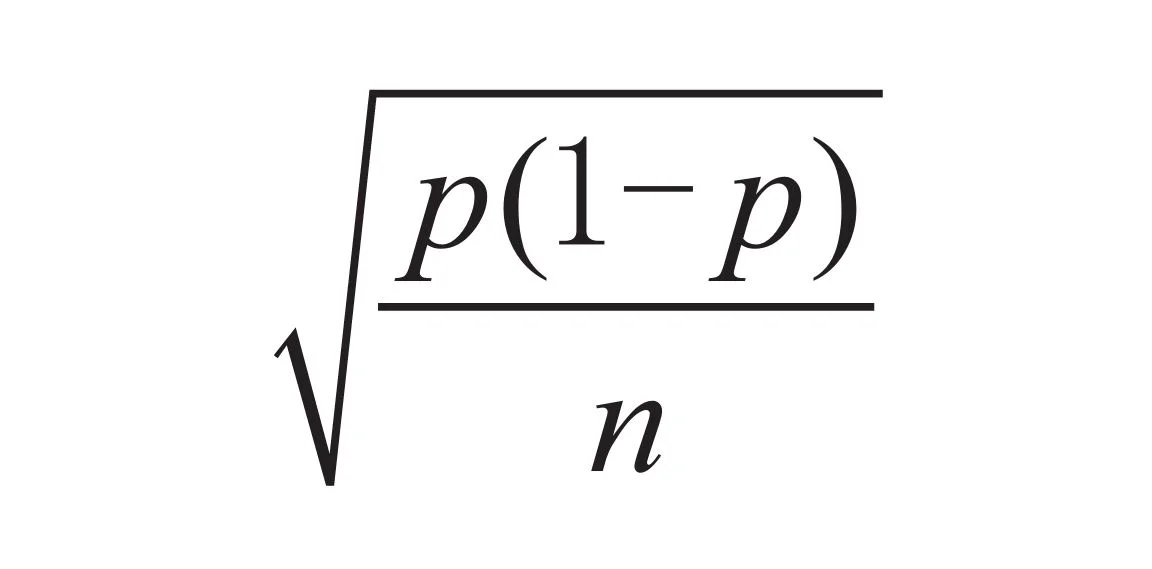
1702638887
1702638888
1702638889
这些事实是可以用数学方法证明的,所以基础很坚实。图21-1把这些事实用某种形式进行了整合,这提醒我们:抽样分布描述的是从同一总体中抽出的许多样本的结果。
1702638890
1702638891


1702638892
1702638893
1702638894
图21-1 从一个成功比例为p的总体中抽取大小为n的简单随机样本,重复抽取许多次。样本统计量的值呈正态分布