1702638861
1702638862
95%置信区间
1702638863
1702638864


1702638865


1702638866


1702638867
我们要估计总体成员中拥有某种特征的比例p,这个特征可能是他们有工作,或者他们对总统的表现满意等。让我们把正在考虑的这个特征叫作“成功”。我们会用简单随机样本的成功比例,来估计总体的成功比例p。样本统计量作为总体参数p的估计值,表现如何?想要得到答案,我们应该问:“如果我们取许多个样本,会发生什么情况?”我们知道,的值会随样本而变,我们也知道这个变异性不是偶发的。长期下来,它有很清楚的形态,用正态曲线可以把这个形态比较准确地描绘出来。
1702638868
1702638869
样本统计量的抽样分布
1702638870
1702638871


1702638872
样本统计量的抽样分布,是指从同一总体中抽出的同样大小的所有可能样本,其统计量之值的分布。从一个成功比例为p的很大的总体中抽取一个大小为n的简单随机样本,用表示成功的样本统计量:
1702638873
1702638874


1702638875
1702638876
1702638877
当样本够大时,
1702638878
1702638879


1702638880
•的分布接近于正态分布。
1702638881
1702638882
• 抽样分布的平均数和p相等。
1702638883
1702638884
• 抽样分布的标准差是:
1702638885
1702638886
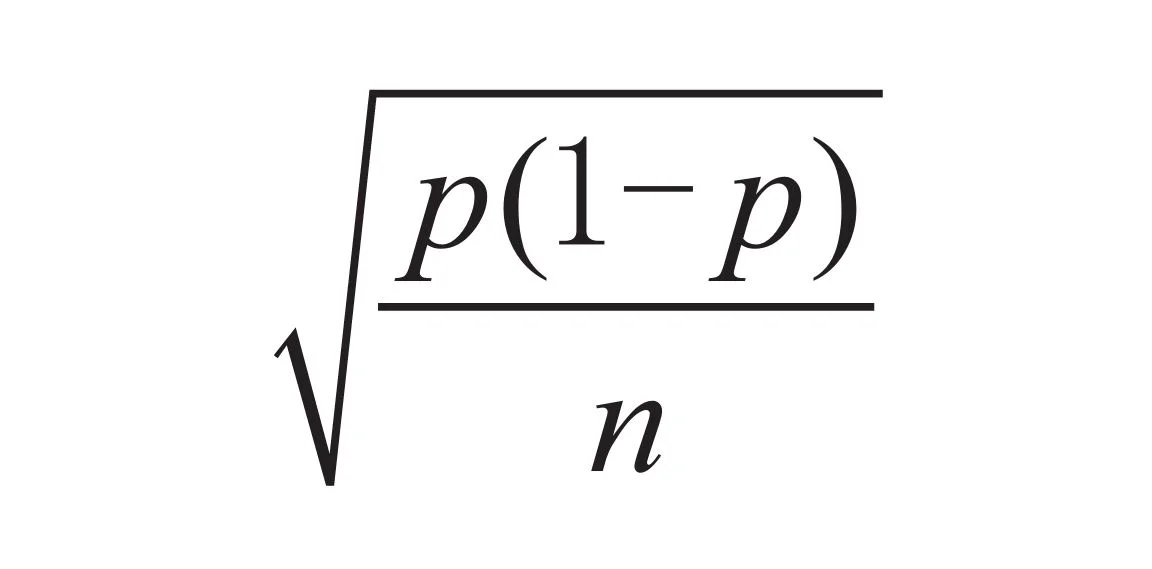
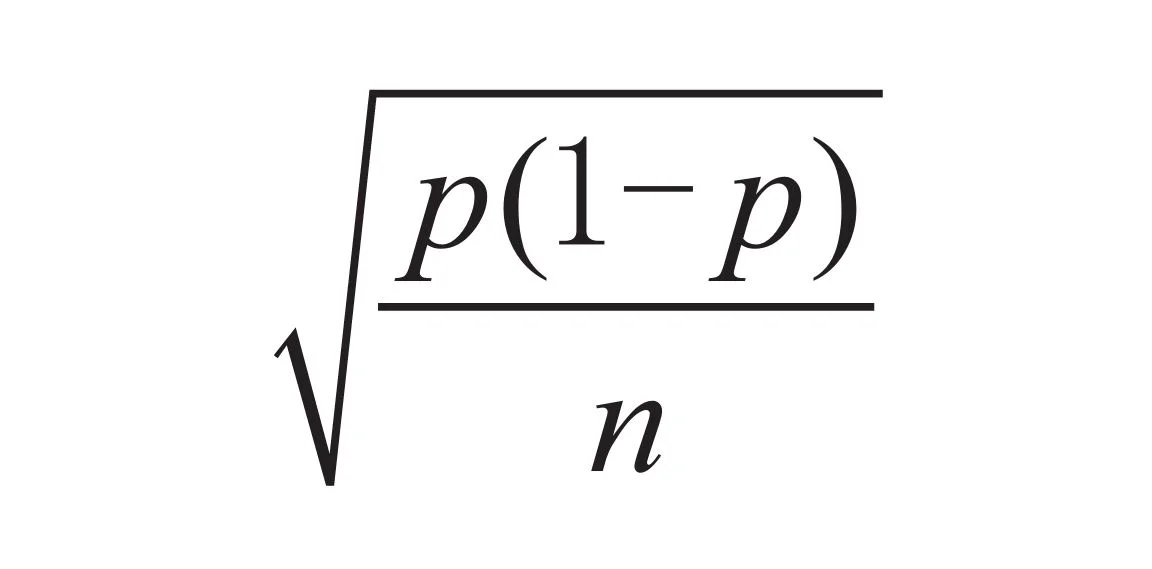
1702638887
1702638888
1702638889
这些事实是可以用数学方法证明的,所以基础很坚实。图21-1把这些事实用某种形式进行了整合,这提醒我们:抽样分布描述的是从同一总体中抽出的许多样本的结果。
1702638890
1702638891


1702638892
1702638893
1702638894
图21-1 从一个成功比例为p的总体中抽取大小为n的简单随机样本,重复抽取许多次。样本统计量的值呈正态分布
1702638895
1702638896
例2 酗酒问题
1702638897
1702638898


1702638899
假设12%是2010年加州全体大学生的酗酒人数比例,那么在例1中,p=0.12。BRFSS的样本大小n=6911,如果重复抽样很多次,样本比例会很接近正态分布,其平均数=p=0.12。
1702638900
1702638901


1702638902
1702638903
1702638904


1702638905
这个正态分布的中心是对这个总体的正确描述。由于样本非常大,所以标准差很小,几乎所有样本都将产生一个非常接近真实参数p的统计量。根据68-95-99.7规则,95%的样本统计量将落在平均数减去两个标准差(0.12-0.0078=0.1122)和平均数加上两个标准差(0.12+0.0078=0.1278)的区间内。见图21-2。
1702638906
1702638907


1702638908
1702638909
1702638910
图21-2 从成功比例p=0.12的总体中抽取大小为6911的简单随机样本许多个,95%的样本统计量会落在0.1122~0.1278的区间内