1702906856
p的提案者同F就a达成协定可以表示为
1702906857
1702906858


1702906859
1702906860
1702906861
同样,对于外国政府而言,其函数是
1702906862
1702906863


1702906864
1702906865
1702906866
均衡概念
1702906867
1702906868
我们所使用的均衡概念是修正过的序贯均衡(sequential equilibrium)概念(Kreps and Wilson 1982),不完全信息同前面一节所采用的子博弈完美均衡(subgame perfection equilibrium)相类似。
1702906869
1702906870


1702906871
定义:本博弈的修正序贯均衡包括四重战略(),后验信念μ*要共同满足:
1702906872
1702906873


1702906874


1702906875
(1)
1702906876
1702906877


1702906878


1702906879


1702906880
(2),每当
1702906881
1702906882


1702906883


1702906884


1702906885
(3),每当
1702906886
1702906887


1702906888


1702906889
(4)在给定先验信念满足贝叶斯法则,也就是,就有
1702906890
1702906891


1702906892
1702906893
1702906894


1702906895


1702906896


1702906897


1702906898
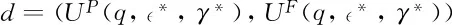
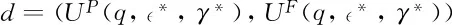
1702906899
一项均衡具有四个特征。首先,行政机构和外国政府在约束条件下(正如之前情况)在条约集合内提出供批准的点,同时也是双方条约谈判的纳什谈判解。对任意均衡(),我们重新界定集合;和不同意点。这样再次设定了一个谈判问题。第二,背书人只会在协定最优条件下具有可能支持协定。第三,选择者只会在给定信念条件下这些条约为最优情况下批准条约。第四,信念同贝叶斯法则和所传递的信息一致。
1702906900
1702906901
需要注意之前的μ不是源于之前的Ξ,而是Ψ。请注意C并不知道f的相对地位。但是,C了解p,也清楚f在支持区间[-1,1]内独立地源自Ξ,而且一旦选定,P和F会在可批准的条约集合内谈判纳什解。那么,什么构成了C对提出的协定的先验信念?我们通过P和F从协定集合中选择NBS的常识,把对提出的协定的这些信念的简化模式视为分配性函数Ψ,Ψ来自Ξ;也就是Ψ(a′)代表了选择者之前的信念:P和F已谈判达成一项政策a′或者小于概率Ψ(a′)的政策。这是我们把信念结构从类型变成协定的方式,也是把偏好转化为政策的方式。这一简化模型的密度记为ψ。但是回想纳什谈判解取决于预期:P和F在谈判时已然知道他们的提案要接受背书人的检验,而且像立法机构的选择者会根据这些背书来最优选择。因此,Ψ是在作出背书之前关于协定的信念陈述。但是在谈判已经开始之后,它就不再是先验信念的陈述,也不是后验信念。然后,这些信念确实在定义序贯均衡上发挥作用,也是因为这个原因,我们可以将其称为暂时信念(interim beliefs)。
1702906902
1702906903
盲目接受的结果
1702906904
1702906905
当博弈是不完全信息的,并且没有背书者,均衡结果如下: