1703624498
1703624499
表7-10 加权久期归因分析
1703624500
1703624501


1703624502
1703624503
1703624504
几何法固定收益归因分析
1703624505
1703624506
尽管Van Breukelen采用了一种算术法归因分析模型,但它可以很容易被转换为几何法。在图7-3中展示了对表7-1数据采用四步决策的流程,每步之间收益率的几何法差别就是该步骤的影响。表7-11中计算了几何法总久期配置的影响。
1703624507
1703624508


1703624509
1703624510
1703624511
图7-3 几何法固定收益归因分析
1703624512
1703624513
表7-11 总久期配置影响(几何法)
1703624514
1703624515


1703624516
1703624517
1703624518
在表7-12中计算了市场配置影响,同时根据总久期影响和可预测的无风险收益率配置贡献对它进行了调整(在这个例子中忽略了货币影响)。由于投资组合权重(市场配置的一部分)决定不同利率的配置,所以市场配置和无风险收益率配置被合并成一步。
1703624519
1703624520
表7-12 几何法市场配置影响
1703624521
1703624522


1703624523
1703624524
1703624525


1703624526
是修正的半名义基金收益率,它表示市场配置步骤的合并影响。表7-13中计算了证券选择影响。为了计算证券选择影响,作为将收益率的变化应用于加权久期的另一个选择,我们也可以将参考基准收益率根据投资组合久期来调整。对表7-14所示的几何法归因分析结果的解释同算术法的例子基本一致。
1703624527
1703624528
表7-13 几何法证券选择影响
1703624529
1703624530


1703624531
1703624532
1703624533
表7-13 几何法加权久期归因分析
1703624534
1703624535


1703624536
1703624537
1703624538
Campisi框架
1703624539
1703624540
采用同Van Breukelen法以及Wagner和Tito法类似的概念,Campisi(2000)提出将固定收益投资组合的收益率分解为利息收入和价格收益,具体如图7-4所示。
1703624541
1703624542
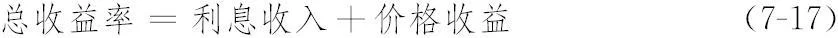
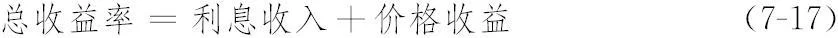
1703624543
1703624544
1703624545
式中
1703624546
1703624547

