1703625036
不像算术法多时段归因分析,随着测量区间的扩展,没有必要去做连续的调整。总的归因分析可以通过复利化得到,具体如表8-17所示。
1703625037
1703625038
表8-17 多时段几何法归因分析
1703625039
1703625040


1703625041
1703625042
1703625043
实际上,几何法的总归因影响几何等同于Davies和Laker算术法归因影响,具体如表8-18所示。
1703625044
1703625045
表8-18 几何法总影响
1703625046
1703625047


1703625048
1703625049
1703625050
每个时段的总几何法归因影响不需要被调整。在每个时段内,每个资产类别的归因影响相加得到总几何法归因影响,所以,每个资产类别的未调整的归因影响不能像总几何法收益率一样的复利化。必要时,单独的资产类别的影响可以被调整,然后它们可以按照式(8-27)复利化以得到总归因影响。
1703625051
1703625052


1703625053
1703625054
1703625055


1703625056
式中 ——资产类别i的调整后的几何法影响。
1703625057
1703625058
在表8-19中,计算了第1季度调整股票选择后的几何法影响。由于调整较小,所以如果测量区间扩展了,也不需要改变。
1703625059
1703625060
表8-19 调整后的股票选择影响
1703625061
1703625062


1703625063
1703625064
1703625065
对于大多数的情景来说,链接方法的选择通常不会改变结果的解释。我偏爱几何法超额收益率,所以我更愿意采用几何法链接。对于算术法超额收益率,我更喜欢GRAP法或Frongello法。
1703625066
1703625067
超额收益率的年化
1703625068
1703625069
就像投资组合收益率和参考基准收益率一样,超额收益率也能够(和应该)被年化。几何法超额收益率对于多时段可以自然地被复利化,但算术法超额收益率无法做到这一点。我们在表2-24的数据中引入了参考基准数据和相应的超额收益率数据,具体如表8-20所示。
1703625070
1703625071
表8-20 年化的超额收益率
1703625072
1703625073


1703625074
1703625075
1703625076
归因分析年化
1703625077
1703625078
使用式(6-23)来扩展式(8-26)以包括货币影响:
1703625079
1703625080
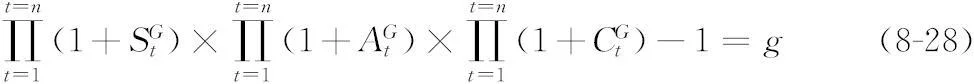
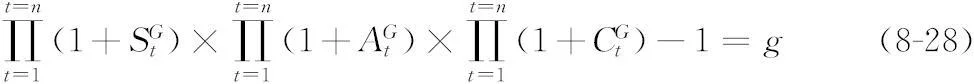
1703625081
1703625082
1703625083


1703625084
式中 ——时段t的总货币几何法归因影响。
1703625085