1704637600
但是,由于生产技术是呈规模报酬递增的,我们会有
1704637601
1704637602


1704637603
1704637604
1704637605
不等式(7.57)两边都乘上p,各减去(r·tx′),有
1704637606
1704637607


1704637608
1704637609
1704637610
但这就与x′与y′=f(x′)已使利润最大的前提相矛盾。因此,只要有规模报酬递增,就不会存在利润函数。
1704637611
1704637612
同理可证,若规模报酬不变,又有利润最大值,则该利润必为零。
1704637613
1704637614
二、利润函数的性质
1704637615
1704637616


1704637617


1704637618


1704637619


1704637620


1704637621
【定理】 如果生产函数在定义域上是连续,严格递增,且严格拟凹〔1〕,f(0)=0,那么,对于产品价格投入品价格集利润函数π(p,r)是连续的,并且有:
1704637622
1704637623
(1)对于p递增;
1704637624
1704637625
(2)对于r递增;
1704637626
1704637627
(3)对于(p,r)是一次幂齐次的(k=1);
1704637628
1704637629
(4)对于(p,r)是凸;
1704637630
1704637631
(5)当(p,r)≫0时,对(p,r)是可导的,并且有霍太林引理
1704637632
1704637633


1704637634
1704637635
1704637636
证明:
1704637637
1704637638


1704637639
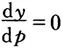
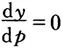
1704637640
(1)按“包络定理”,(因y已是保证利润最大的最优产出选择,⇒);
1704637641
1704637642


1704637643


1704637644
(2)也按“包络定理”,(因xi已是保证利润最大的最优投入选择,⇒);
1704637645
1704637646


1704637647
(3)所以,k=1。
1704637648
1704637649

