1704637650
(4)凸函数的性质是,对有
1704637651
1704637652


1704637653
1704637654
1704637655


1704637656
1704637657
1704637658
图7.6 利润函数的凸性
1704637659
1704637660
我们定义
1704637661
1704637662


1704637663
1704637664
1704637665
令y*与x*使利润在(pt,rt)时最大,于是
1704637666
1704637667


1704637668
1704637669
1704637670
(因为y*与x*在(p,r)时并不保证使π最大)
1704637671
1704637672


1704637673
同理
1704637674
1704637675


1704637676
这样
1704637677
1704637678
这说明利润函数是关于(p,r)的凸函数。
1704637679
1704637680


1704637681


1704637682
(5)(因为y是使利润最大的最优产量选择,所以);
1704637683
1704637684


1704637685
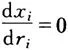
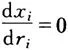
1704637686


1704637687
(因为x是使利润最大的最优投入品选择,所以)。于是
1704637688
1704637689
y*(p,r)即为供给函数。xi(p,r)为要素需求函数。
1704637690
1704637691
(证毕)
1704637692
1704637693
三、供给函数的求法
1704637694
1704637695
事实上,我们至少有三种求供给函数的办法:
1704637696
1704637697
1.从利润函数求供给函数
1704637698
1704637699
由霍太林引理知,要求一家企业的供给函数,若已知生产函数形状,则第一步是求出该企业的利润函数;第二步是让利润函数对产品价格p求一阶偏导,结果就是供给函数。供给函数表达的是供给量y与产品价(p)及投入品价格集(r)之间的对应关系。