1707459547
1707459548
这是一个全新的视角,柏拉图由此来审视算术和其他全部数学科学的文化价值。[302]我们不必指望柏拉图讨论数学问题的具体内容,甚至详细说明研究过程。就像对体育和“音乐”那样,他只是给出了最大胆的概述,用以阐明我们对待数学科目的精神。他顺次提到了各种不同的数学训练。因此,在他的概述中有不少重复之处,因为在处理其中每一个时,他都想把自己的观点再讲一遍:即数学公认具有促进“思想”的特点。他承认,迄今为止,数学从未被用于这一目的。(我们可以回想一下,我们关于智术师的数学教育以及他们为此给出的现实主义理由所说的话。[512] )柏拉图接受了智术师对数学的高度评价,但他没有遵循他们把数学的价值置于其实用性之上的做法。当柏拉图说数学对战略很有价值时,他只是在对他所规划的统治者的教育做一种让步;未来的政治家上升到哲学的旅程是如此艰难,以至于他理所当然地认为,他们对文化极其热爱,[否则,他们根本不可能踏上这一旅程]——这种纯粹的爱是如此丰盈,以至于当柏拉图提到这些研究和学习的实际意义时,他几乎不会想到它会有损他为研究数学所给出的真正理由。[513] 柏拉图尤其嘲笑那些讨论几何学的数学家:他说他们的行为“非常可笑”,他们在排列自己的证据时好像几何运算只关乎实际操作(praxis),而非知识(gnosis)。[514] 柏拉图用大量令人印象深刻的比喻——这些比喻都指向同一方向——三番五次地将数学知识描述为将灵魂导向思想、净化和点燃灵魂、召唤和唤醒理性的力量。[515] 将要统治理想城邦的青年男女不仅要有一种非专业人员的数学知识,而且还要有一种专业人员的数学知识。[516] 他们必须学会欣赏科学的美及其有用性,不是为了像商人和小贩那样做买卖,而是为了有助于灵魂“转向”超越的实在。柏拉图认为,算术的影响是使一个擅长算术的人能够理解科学的全部分支;而学习迟钝的人接受了算术训练之后,即使他在其中没有得到任何好处,至少他们的理解力也会变得敏锐。[517] 数学是一个很难的科目,那些先天条件最好的智力精英必须接受数学的教育。
1707459549
1707459550
除了算术和几何,智术师教育体系中的数学分支还包括天文和音乐。[303]这整个组合后来被称为“四艺(Quadrivium)”。[518] 至于柏拉图是从智术师传统还是从别的来源接过这一教学方案的,我们不是十分清楚。在《王制》中,当柏拉图从天文过渡到音乐时,他提到毕达哥拉派的人相信天文和声乐是姐妹科学。[519] 我们可以由此推论,将这两门学科与算术和几何联系起来的也是毕达哥拉斯派的人,或者至少为他们所知。至于我们是否能够更进一步把为希腊人所知的全部精确科学都归功于以阿尔基塔斯(Archytas)为中心的毕达哥拉斯派,是另一个问题。也许不能;但至少他们大力鼓励这些“数学因素涉及物(mathemata)”的学习,而柏拉图曾经与他们过从甚密。[520] 在讨论数学在他的哲学教育范围内所起的作用时,柏拉图谈论他们时尊敬有加,把他们称为知识的这个分支中的最大权威。尽管如此,柏拉图仍然批评他们执着于感官知觉,而不是继续前进,将心灵集中于纯粹的思想之上。[521] 他们是音乐方面的专家,因此,尽管他们对柏拉图帮助极多,但是,是柏拉图自己提出了支配其思想的观点。他在讨论音乐时明确地表达了这一点——“音乐”一词他在这里指的不是器乐的教学,而是指和声的理论。他说,毕达哥拉斯学派的人对可以听见的一切和声和音调进行无休止的测量和对比,试图发现它们中间相应的数字;[522] 但是,他们在“难题”的开端就止步不前了,[523] 柏拉图相信,不仅是音乐中的,而且还有几何和天文中的这些难题,都是他的教育体系想要研究的问题。[524] 以此种意义上的“难题”,柏拉图意指直接导致对事物本身——即无形体的存在(Being)——的沉思的那些困惑。毕达哥拉斯学派并不是在寻找向上的道路,不问“哪些数字是和谐的数字,哪些又不是,它们又为什么是这样”。[525] 他们并不从柏拉图所建议的角度研究数学的全部对象的相互关系;他们没有回到它们全部具有的共同基础之中;[526] 他们只是得到了对数线面、天空中看得见的现象、听得见的声音与谐音的一些分散的观察。因此,柏拉图说,如果我们只考虑日月星辰这些有形事物的运行和看得见的数量关系,就会很难相信天空中的现象是永恒的、相互之间永远遵循同一比例,当此之时,他批评的正是毕达哥拉斯派的天文学。[527] [304]这些批评含有这样的意思:柏拉图这样做,是在为他自己某部特定著作中的理论的正面阐述节省力气,这些批评引出了我们在《蒂迈欧》和《法义》中再次遇到的合乎逻辑的结论:即天体运行现象中的数学的规律性,预设了在天上安排和引导它们的灵魂的存在。[528] 不过,由于柏拉图正集中注意力于教育问题,他在这里克制自己,没有深入这些科学细节的探讨——即使在讨论自己的哲学时,他也总是遵守着其大略的原则。[529]
1707459551
1707459552
柏拉图可以毫不费力地将所有这些特殊科目的知识——对这些科目的知识,柏拉图只是叙其大略,而非详尽阐释——归到苏格拉底头上。苏格拉底似乎总是无所不知,通晓每一个讨论中出现的科目;尽管他好像聚精会神于中心主题,但是,对于我们本来认为他可能所知甚少的那些科目,不时表现出惊人的熟悉。苏格拉底的这种无所不知必有其历史根源,但有一个事实毋庸置疑那就是,真实的苏格拉底并未对数学各科看得如此之重——柏拉图在此力图使它们成为通往“善[好]”的知识的“道路”。这一事实是一个很好的试纸,它证明了柏拉图在写作其对话时,可以完全自由地将自己的思想置于苏格拉底之口。当色诺芬说苏格拉底对数学略知一二,但认为其教育价值受到其实用性的严格限制时,他针对的显然是柏拉图对这一事实的非历史态度。[530] 这当然与柏拉图让苏格拉底说的正好相反。色诺芬有意驳斥柏拉图这一事实,可以用来证明真正坚持历史事实的是色诺芬,而不是柏拉图。历史上的苏格拉底可能从未像柏拉图笔下的苏格拉底那样责备他的对话者,因为这些对话者通过宣称天文学在农业、航海和战略上的实用性来证明天文学的正当性。[531] 这里,即使在对苏格拉底的思想的理论阐述中,柏拉图的教育也显示了他所赋予数学的那种重大意义。尽管柏拉图自己指出,数学对一个战略家来说不可或缺,但他对科学的任何纯实用主义考虑都持怀疑态度。就像天文学(它被当作数学来看待)教导我们做的那样,灵魂要“向上看”,但这种“向上看”与把目光像专业的天文学家那样转向天空大不相同。[532] [305]灵魂中“向上看”的那个部分“比一万只眼睛都重要”,柏拉图教育体系中学习的数学会将它点燃,使它纯净和明亮。[533]
1707459553
1707459554
柏拉图没有遵循传统的说法认为数学只有四个分支。他介绍了一门他自己称之为崭新的数学学科:立体测量学。[534] 排在几何学之后的天文学的位置,必定在他那个时代得到了重新安排。似乎是为了遵循常规的习惯,柏拉图在第三的位置说到了几何学,并开始对它的讨论;[535] 不过,他马上纠正自己,说按顺序接下来应该是关于空间中的物体的科学,这与一切立方体和有厚度的东西有关,因此,它应该跟随在研究线和面的几何学之后,处在研究星体运行的天文学之前。[536] 立体测量学的引进是个惊喜,柏拉图因此为这个部分带来了某种变化。很明显,柏拉图此处的思路受到学园日常教学步骤的影响。古代晚期的数学史家,利用一种传说——这一传说可以追溯到亚里士多德的学生优台谟(Eudemus)的一部基础著作——声称是泰阿泰德引进了立体测量学。泰阿泰德是雅典杰出的数学家,柏拉图在《王制》发表数年之后,以泰阿泰德为名写了一部对话。[537] 我们现在认为,他于公元前369年在军队服役时死于流行性痢疾。[538] 欧几里德(Euclid)的《几何原本》(Elements )是全部希腊数学的永恒基础,其最后一章(第十三章)中关于立体几何的思想只在泰阿泰德一代人之后就写就了,因而必定曾是泰阿泰德的基本思想。[539] 他在学园中是一个众所周知的人物。在《泰阿泰德》中,作为一个和蔼可亲的学者,柏拉图给他画了一幅招人喜爱的肖像。毫无疑问,是泰阿泰德的个人影响力促使柏拉图在《王制》中给了他所创立的科学以如此光荣的地位。
1707459555
1707459556
对我们来说,在研究柏拉图的教育(paideia)时,利用这一重要机会评估柏拉图本人对《王制》中各种哲学教育方案的实际科学兴趣至关重要。自欧几里德确立数学的经典形式——也即科学的形式(其基本原则一直行之有效)——以来,已经过去了二千多年,我们已经很难追溯那个才智迸发的时代——其时,数学的形式仍在向着其最终目标奋力前行。如果我们记得这只是相对较少的几代人的工作,我们就会意识到,少数杰出科学家聚精会神的思考是如何创造了一种胜券在握的自信气氛——这些科学家相互之间激烈竞争,[306]争先恐后地推进自己的学科,在公元前四世纪雅典智识生活无处不在的兴奋不已中,这种氛围注定会对哲学思想产生回应。对哲人而言,数学看起来是一门理想的学科:逻辑推理和证明的一种严谨而牢不可破的结构,某种前苏格拉底自然哲学家们的时代做梦也想不到的东西。数学家们后来对科学方法的发展给予的关注,增添了数学作为新科学的范式的价值——这种新科学是由柏拉图从苏格拉底关于德性的对话中辩证地发展出来的。如果没有同时代的科学(通过提出新问题和解决问题的新方法)对哲学的深厚影响,那么与其他大哲学家一样,柏拉图不可能形成他的哲学。数学对柏拉图的启发和激励仅次于医学(我们已经三番五次地指出医学对他的影响)。柏拉图从医学那里得到了人的身心状态(状态=hexis )之间的类比,以及哲学应该是一种技艺、一种与医术相当的技术、一门关于灵魂健康的科学的观念。数学向他展示了,理性是如何与只可知而不可见的事物(如型)一起运作的。另一方面,柏拉图自己以其新的逻辑发现,大力鼓励数学家们将他们自己的科学建构为一种系统的结构——因此,正如古代传统所告诉我们的那样,它们之间是相辅相成、相互受益的关系。[540]
1707459557
1707459558
泰阿泰德对柏拉图变得重要是在他人生中相对较晚的时期。当泰阿泰德于公元前369年去世时,柏拉图仍处于人生之盛年:因此,当柏拉图在数年之前将他的那些发现写进《王制》时,它们必定相当新颖。[541] 柏拉图与数学的首次接触,甚至在他遇到毕达哥拉斯派的人之前,必定早就发生了,因为像《普罗泰戈拉》和《高尔吉亚》这样的对话——这些对话透露出作者对所论及的学科的明显兴趣——在柏拉图首次西西里之行前就写就了。在这一时期的雅典,必定有大量研究数学的机会。[542] 不幸的是,我们不能深入追究柏拉图与昔兰尼(Cyrene)之间的关联,据说柏拉图在苏格拉底死后曾经访问过这个城市(尽管这一说法没有得到证实)。[543] 后来,当柏拉图写作《泰阿泰德》时,将泰阿泰德本人(他代表数学家中乐于接受哲学问题的年轻一代)与一名年长者[307](即昔兰尼的西奥多鲁斯[Theodorus],他是一位声名卓著的科学家,但对哲学问题无甚兴趣)作对比。这也似乎暗示了柏拉图对西奥多鲁斯有一些个人的了解。[544] 公元前388年的南意大利之旅,柏拉图遇到了当时毕达哥拉斯派的主要学者。可能其中之一就是塔伦特姆的阿尔基塔斯(Archytas of Tarentum),他是一位政治家、数学家、毕达哥拉斯派中最杰出的科学家。柏拉图和他共处了一段时间,并成了他的终生好友。[545] 确实,柏拉图的哲人教育的理想就是以他为基础建立的,他是活的原型。亚里士多德说,柏拉图的研究和教学体系本质上是对毕达哥拉斯派的模仿,尽管其中也包含着一些他自己的东西;这一引人注目的说法肯定主要是指他教学中的数学方面——这个方面在对话中并不突出,但在柏拉图学园中却扮演着重要角色。[546] 希腊传记作者关于亚里士多德的记叙——即亚氏进入柏拉图的学校时,“比欧多克索斯年轻(under Eudoxus)”——允许我们做出一个推论。亚里士多德经常连同学园一起提到大数学家欧多克索斯;亚里士多德在《伦理学》(Ethics )中说他本人认识欧多克索斯。因此,在亚里士多德本人进入学园时(公元前367年),欧多克索斯有一段时间肯定经常前往柏拉图学园。[547] 欧多克索斯自己的学校在基济科斯(Cyzicus),它与柏拉图学园的联系一直保持到下一代。[548] 这是柏拉图学派在数学进步中所起的积极作用的显著证据。柏拉图晚年的秘书和最亲近的助手是奥普斯的菲利普,他是柏拉图遗著《法义》的编辑者,我们已经提到过他;他也是古代著名的数学家和天文学家,而且著述颇丰。[549] 看来,他跟赫尔谟多罗(Hermodorus)和赫拉克利德斯(Heracleides)一起,是柏拉图学园中关于这些学科的主要权威之一。不过,赫拉克利德斯的研究似乎更多地代表的是天文学方面的沉思,菲利普是典型的研修生,尽管在《厄庇诺米斯》中(像所有柏拉图主义者一样),他将天文学看作神学的基础。
1707459559
1707459560
这些事实是对我们的一种警醒,使我们记得,柏拉图的著作无非是学园的科学研究和教学的一种反映,它们显示了学园的内在结构。《王制》中提供的数学教学规则,[308]明确表明了数学在学园的哲学课程中所处的地位。很明显,柏拉图没有在研究和教学之间作出区分。整个知识领域清晰可见,因此,他只是引导未来的统治者研究整个学科,[550] 没有做任何挑选,他甚至欢迎像立体测量学这样的新生分支来扩展自己的课程计划。关于政治家的正确教育,我们很容易想像其他学校肯定有不同的想法。在任何抱着一种实用目的,也即修辞学[雄辩术]的目的的地方,比如在伊索克拉底的学校中,柏拉图对精确的数学知识在政治教育中的评价,肯定是太过夸大其词了,他们更多强调的肯定是经验的重要性。不过,柏拉图因为大力发展数学而遭受批评这一事实,强烈地表明了柏拉图将数学作为其教育体系的拱顶石。
1707459561
1707459562
无论是在较为简单的卫士教育中,还是在教育的这种高级形式中,柏拉图的教化都没有建立在纯粹的理论之上。在城邦卫士的教育中,他接受所有现存的传统文化(柏拉图以此指希腊文化),即民族的全部诗歌和音乐,作为教育的主要材料;只是他迫使这些材料净化自身,并准备实现其最高使命。在后者中,他将同时代科学的源头活水引入自己哲学教育的沟渠;只是他搜寻出可以为他的哲学目的直接服务的任何东西,并使其从属于这一目的。这引出了另一个问题:柏拉图对那些在他的教学方案中没有提到的其他学科抱何种态度呢?如今,我们相信,科学的边界肯定不比人类经验的边界狭窄。这会使我们认为,柏拉图的教化给予数学的巨大声望是对重点的一种严重扭曲,或者,也许这是因为数学在柏拉图时代的支配地位。不过,尽管数学在学园中的首要地位肯定归功于那些孜孜以求的大家,以及他们所带来的自信感和进步,但它的重要性归根到底还是基于柏拉图哲学及其知识观念的特征。柏拉图将一切经验知识排除在教育之外。智术师试图培养百科全书式的“学术研究(scholarship)”的尝试,在柏拉图的学校中没有得到进一步的发展。[309]在同时代的阿提卡谐剧的残篇中,我们发现了一些玩笑,这些玩笑针对柏拉图及其学生在讨论如何界定与划分植物和动物时的冗长乏味的辩论。这些间接提示证实了我们从柏拉图的对话中得出的印象。是谐剧家厄庇克拉特(Epicrates)的笑话给学园教学的秘传秘密投下了一道亮眼的侧光,尽管夸大其词,但他提出了正确的观点。哲学家们确实对植物所知不多,在试图对植物进行分类时,他们显得相当荒唐可笑——其可笑程度足以娱乐雅典剧场的观众。厄庇克拉特曾让一位西西里的名医(因而是经验知识的代表人物)——他碰巧参加了这些讨论——一言不发但粗鲁无礼地表达了他对此类讨论的厌倦,他的这种表达方式适合于一个“未受教育的自然主义者”。由于他所参与的是动物学和植物学研究,一些读者曾经错误地推论,学园中的教学实质上必定与《王制》里所描述的大不相同,学园中的教学活动必定给予经验知识以极大关注。[551] 不过,如果没有观察,即使是动植物分类的深入研究,也是无法完成的(尤其是如果这种研究旨在一种完整的系统性的话),学园中的科学家们绝不会试图收集所有已知的各种草木鸟兽,他们要做的是分门别类,然后在一个涵盖“一切存在物”的巨大逻辑框架内将它们纳入正确的位置——就像在柏拉图的后期对话中关于其他学科所做的那样。这些具体科学研究的真正目的是辩证法。如果柏拉图在《王制》中关于教育方法的叙述未曾给我们留下相同的印象,那是因为(如我们前述已经指出的那样)他只是概述了教育各阶段的大略而已。因此,厄庇克拉特间接提到的动植物分类应该被置于《王制》教育方案的第二部分,即紧随在数学之后处理辩证法的部分。
1707459563
1707459564
辩证法中的教育
1707459565
1707459566
苏格拉底的对话者告诉他,迄今为止,他所设计的全部课程都极其困难。作为回答,柏拉图让苏格拉底将其比作一首主曲(一种独唱曲)的前奏曲,[310]从而表明他所达到的程度,以及向最高阶段的转变。[552] 数学只不过是我们现在要学习的主曲的序曲而已。即使此间的专家,也算不上辩证法家。柏拉图暗示自己平生几乎未曾遇到过也是辩证法家的数学家。泰阿泰德是其中的凤毛麟角之一。在一部以他的名字命名的对话中,柏拉图刻画了新型的哲学的数学家形象(如我们前述所言);与此同时,通过讨论数学和哲学共同具有的知识的大问题,他表明了一个训练有素的数学家是如何经由辩证矛盾通向哲学的知识的。苏格拉底的主要对话者是一个天资聪颖而又急于求知的年轻数学家,这不只是一种巧合。柏拉图意在告诉人们,辩证法教育对那些做了最佳准备的人的影响究竟如何。《泰阿泰德》也表明,哲学的领悟与数学以及漫长而艰辛的教育成果相互关联。[553] 这篇晚于《王制》数年的对话,读起来像是对《王制》中给出的、经由辩证法的哲学教育的描述的一个延伸性解释。在制定教育的规则时,柏拉图无法为较早阶段的教育提供事例,当然,也无法提供辩证法的事例。相反,在其他所有的柏拉图对话中都有相关事例,它们记录了对某些特定问题的辩证探究,过程的本质对跟随它并观察其逻辑结果的读者而言完全一清二楚。但是,赋予柏拉图的描述——他在《王制》中将辩证法教育描述为教育的最高阶段——以特别的兴趣和魅力的,是柏拉图对他自己的发现的态度,以及他将这些发现的价值和问题作为一种教育的手段来描述的努力——在他二十五年的经验的基础上。
1707459567
1707459568
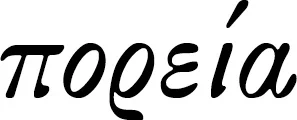
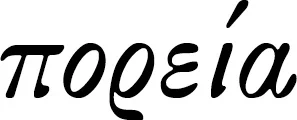
1707459569
即使在这里,在辩证法的定义方面,柏拉图所提供的也不比我们从早期对话中已经知道的更多。就在教育的这一最后阶段的开头,他将辩证法定义为“提出某种论点并对之作出解释的能力”,并由此提出了它的起源。[554] 这个定义不过是苏格拉底的老方法的传统描述,苏格拉底的方法就是通过与别人的论辩和辩驳,即“辩驳论证(elenchos)”,来达到共识的方法,柏拉图的逻辑理论和辩证法技艺就是从中生长出来的。[555] 柏拉图明确认为,他在苏格拉底的谈话中所感受到的那种巨大的转化力量,[311]证明了辩证法哲学乃是真正的教育这一主张的合理性。从这一高度看,教育的第一阶段,即数学,就下沉为一种前期教育(propaideia)。[556] 但是,什么才是我们在数学这一序曲中首次聆听、然后又在辩证法中得以完成的“主曲”呢?为了理解它是什么,我们必须回到柏拉图的洞穴比喻中去。洞穴比喻是灵魂的上升之旅的一个视觉意象。当灵魂的眼睛转过身来、灵魂离开洞穴进入真实世界之后,它试图看清的,首先是活的动物,然后是星辰,最后是太阳本身。就这样,一步接一步,它学会了看清事物本身,不依赖它之前习惯的阴影。通过辩证法获致知识的人以同样的方式,靠思想而不靠任何感性知觉达到每一事物的本性,直到他透彻地把握住“善[好]本身,善[好]的真正之所是”,并由此达到可知世界的终点——就像太阳,这个洞穴的光源,是可见世界的终点一样。[557] 思想的这一上升“旅程( )”就是辩证法。[558] 已知的全部科学研究的目的,是“把灵魂中最优秀的部分带上去看到最高贵的实在”。[559] 思想到了那里就完成了全部旅程,如同到了道路的尽头。[560] 柏拉图本人感觉到,这一简短的比喻性描述是何等勉强和概括,但他宁愿先将其作为一个大概写下来,因为他还要经常回到辩证法这一主题。[561]
1707459570
1707459571
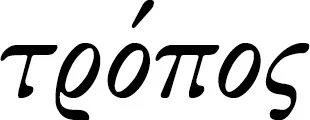
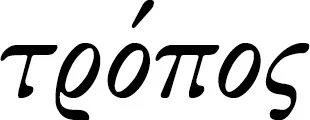
1707459572


1707459573


1707459574


1707459575


1707459576


1707459577


1707459578


1707459579
辩证法的特性( )只有通过它与其他类型的知识的关系来界定。理解事物的本性有许多种方法。经验性的技术,即“技艺”,处理人的意见和欲望:它们或是生产和建造,或是照料( )由艺术或自然产生的事物。[562] 数学的诸分支比较接近真正的实在,但它们可以说只能像做梦一样触及到它,清醒的时候它们不能真正看到它。如前所述,它们从它们无法作出系统解释的假设(hypotheses)开始。因而,它们的“本原(principle)”是它们所不知道的东西;而其他一切东西都是从它们不知道的某种东西中“编织”出来的。这种类型的“一致认可( )”不应该被称为科学或知识( ),尽管我们已经习惯于这样做。[563] 辩证法是一门“排除”其他科学的假设、并直接上升到一切事物的第一本原的科学,在数学的帮助下,[312]它“轻轻地把埋没在原始状态的污泥中的灵魂的眼睛拉出来”,并引导它向上。[564] 我们现在知道了实在和知识的各个不同阶段之间的比例的意义,这个比例是柏拉图早先为了说明其教育目的而给出的。意义就是这个。意见关乎生成,理性关乎存在,理性与意见相对就像存在与生成相对。就像思想与意见相对,所以真正的知识( )与感觉( )的证据相对,数学的思维与可见对象的阴影相对。[565] 换句话说,辩证法给出的知识对数学知识所包含的存在和实在的数量的优越性,就像可见世界中真正的对象对它们的阴影的优越性。因此,辩证法家就是能够理解每一个事物的真正本性并对之作出相应解释的人。[566] 同样,辩证法家必定能将“善[好]的型”从其他一切事物分离( )开来,也就是说,将“凭其本身就是的善[好](good by itself)”与各种具体的事物、人物、行为等等——我们把这些东西叫作善[好](good)——分离开来,用理性(logos)来界定它,就像在战场上“经受住各种攻击”,勇往直前,坚持到战斗的最后阶段,不让他的思想在任何地方绊倒。[567] 这种教育教导人“以最科学的方式提出问题和回答问题”,[568] 它的真正力量在于它使人处于完全清醒和警觉的状态。这就是为什么柏拉图将其称作最高意义上的卫士教育(也就是城邦统治者的教育)的原因。“卫士”对统治阶级来说是一个相当奇怪的名字,柏拉图似乎是着眼于理智警觉性的哲学德性而选择的这个名字,这种理智的警觉性正是城邦的统治者要培养的。[569] “卫士”这个名称首先是给全体战士阶层的,随着选拔的深入进行,它越来越被限定在统治者身上,[570] 他们是参与到高级教育中的少数人。柏拉图说,任何不以接受此种教育为乐的人,都是在睡梦中打发一生,在他醒来之前就进入了哈德斯的世界,并且永远沉睡下去。[571] 在科学的体系中,辩证法是一切学科的盖顶石( ),人类的知识都以此为顶点:没有任何别的学科能比它更高,或者凌驾于它之上。[572] 关于“意义”的知识是关于“存在”的知识的最终目标。
1707459580
1707459581
1707459582
1707459583
1707459584
教化:古希腊文化的理想 哲人的课程
1707459585
1707459586
我们现在可以问,谁适合上升到如此高度,戴上文化的皇冠。当柏拉图在解释如何将卫士训练得具有统治者的德性时,[313]他说,只有那些具备最坚定、最勇敢的天性的人才能被选来作为哲学的统治者,同时他们必须尽可能地英俊、高贵且以此为荣。[573] 不过,他们还必须把这种最优秀的品质(kalokagathia)与那些接受高级教育的必备品质(即目光敏锐、理解迅速、博闻强记和坚韧不拔)相结合。参与辩证法这种敏捷游戏的人,在甘心吃苦方面决不能是一个瘸子。也就是说,他决不能是一个这样的人:他一半甘心吃苦,另一半不愿吃苦,就像一个人喜欢体育和打猎,甘心在一切涉及身体的事情上吃苦,并乐此不疲,但很容易在需要理智劳心费神的事情上放弃,不愿学习、听讲和研究,而且痛恨这类工作。在真假问题上,他决不能只是一个真理的半吊子热爱者——他憎恨存心编造的谎言,不仅不容忍,当别人撒谎时,他还会充满愤怒,但他能容忍无意的不实之词。当他被无知所困扰时,他必须对自己非常恼火,决不能像一头猪一样在无知的污泥中自得其乐。除非他的灵魂与身体一样健康,否则没有人能够称其为统治者。[574] 因此,仅仅只有之前为未来的统治者规定的性格测试是不够的;[575] 必须用一套经过精心设计的人才甄选体系对其进行补充,这样的甄选体系将考察和证实那些适合辩证法学习的人,使他们适得其所。在柏拉图的时代,所有这些想法都是全新的,与对人的健全理智的盲目信任有天渊之别——对人的健全理智的盲目相信,是那些除了日常生活,什么都不学的人的固有特征。自柏拉图时代以来,已经出现了大量的学校和考核情况,尽管我们不能确定,如果柏拉图死而复生,他是否会认为它们之中每一件事情都是他曾经希望的。
1707459587
1707459588


1707459589
为了发现这极少数将要统治理想城邦的男人和女人(也许只有一个),选拔工作必须在人年少时而且在一个很广泛的基础上早早开始。尽管柏拉图之前反对过在人刚刚成年的那几年集中学习哲学的想法,[576] 但他的意思并不是说年轻人根本就不能学习哲学。数学这样的预备性功课,在他们还是孩子时就开始了。[577] 不过,每一种早早开始的教育尝试都会碰到一个巨大的障碍,那就是孩子们不想学习,但我们不能强迫他们学习,因为抱着害怕惩罚的奴隶心态去学习与自由教育的精神完全背道而驰。各种身体锻炼,即使在强迫中得以进行,也不会使身体不如以前,[314]但用暴力强行灌输的知识不能久存于灵魂。[578] 因此,柏拉图明确断言,在教育的这个阶段给孩子们介绍知识,应该像是在玩耍一样。[579] 毫无疑问,柏拉图的这一断言是根据他那个时代不断增长的“填鸭式”教育产生的糟糕结果所得出的,只要那些新兴学科不是只保留给那些最热切、最有天赋的学生,而是想大水漫灌,把它们也灌输给资质平平的普通学生,就会产生这种糟糕结果。甚至柏拉图自己也没有把这个阶段的标准定得太高:他说,组成这些基础教育的游戏,目的是为了显示哪些可能是最有天赋的学生。柏拉图还将这种游戏性的学习体系与同时期付诸实施的其他学习方法相比,这种方法就是将幼儿带到战场观看战斗场景:让他们像幼兽一样“尝尝血腥味”,克服对学习的恐惧心理。[580] 即使在这个阶段,他们也决不机械地学习任何东西。他们的老师应该把适合他们年龄的数学问题“推荐( )”给他们。这是柏拉图首次提到专注于“问题”的学习,这种学习在柏拉图的数学课程的后期高级阶段中会变得越来越明确。[581]
1707459590
1707459591
第一次选拔在完成强制性体育训练之后进行。柏拉图说这种体育训练会持续两三年。在此期间,头脑完全没有得到训练,因为极度疲劳和困倦是学习的大敌。不管怎样,体育锻炼中表现出来的坚韧不拔本身就是一个考察和选拔的重要因素。[582] 智力训练从二十岁重新开始的事实表明,强制性体育训练是在十七岁到二十岁之间——柏拉图将这种强制性训练与早期和晚期的自愿性体育训练相区别。十七到二十这个年龄段是雅典的合格青年作为军校学员(ephéboi)接受训练的时期:他们的服役时间从十八岁开始并持续两年。柏拉图仿效了其时间段,但又觉得有必要再加上一年。[583]
1707459592
1707459593


1707459594


1707459595
此后就开始了另一个教育过程,学生们必须把自己早先分散学到的各门知识统一起来:将各门学科相互比较,直到对“它们的相互关系和存在的本性”达到一种“综合把握(synopsis)”,一种全面而统一的理解。[315]尽管这种综合把握始于数学,但这个阶段的知识不是数学的知识,而是辩证法的知识,因为辩证法家就是能看清不同领域和不同对象的知识之间相互关系的“纵观全局者”(the “synoptic”)。[584] 通过声明选拔出来的学生首先要像在战斗中“坚守到底”一样,在学习中“坚定不移( )”,柏拉图表明他正在把军人荣誉准则的最高戒律转移到理智的领域,就像他总是把他从斯巴达借来的东西转移到一个更高的精神水平一样。[585] 经过十年的辩证法学习,在学生们年满三十岁时,再对那些第一次入选的人进行二次选拔( ),并给他们更大的荣誉。[586] 然后,三十岁到三十五岁的这五年,应该看看他们之中谁能不依赖感官知觉,只靠自己的辩证思维能力就继续前行,跟随真理达到真正的存在(Being)。[587] 柏拉图说,这最后的五年意在与两到三年的强制性体育锻炼相对应。[588] 它们是辩证法的体操训练,其与前十年辩证法的辩驳和综合的学习的关系,就是柏拉图《政治家》和《智术师》中的抽象而系统的辩证法与更基本的早期对话的关系。[589]
1707459596