1700978109


1700978110
1700978111
1700978112
px从零增加到极大值时,N对应降到零.从上式很易确定l=L/2时,px达极大,绳将甩离桌面棱边.
1700978113
1700978114
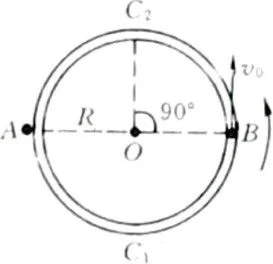
例10 如图3-24所示,半径R的水平凹形圆槽绕着圆周上的A点匀速旋转,在直径AOB的B处放一小球,小球与槽的侧壁光滑接触,与图中AC1B半圆槽底部也光滑接触,与BC2A半圆槽底部有摩擦,摩擦因数处处相同.开始时小球相对圆槽有切向初速v0.小球经过BC2A半圆以近似为零的相对速度通过A点,继而又绕过四分之三圆周到达C2点时速度恰好降为零.
1700978115
1700978116

1700978117
1700978118
1700978119
图 3-24
1700978120
1700978121
(1)试求圆槽绕A点旋转角速度ω和小球与BC2A半圆槽底部间的摩擦因数μ;
1700978122
1700978123
(2)判定小球到达C2点后能否停留在该处,若不能,小球将朝哪一个方向运动?
1700978124
1700978125
解 (1)圆槽参考系是匀速旋转非惯性系,惯性离心力对应离心势能,科里奥利力不作功.将小球初位置B与到达的位置A和后来又到达的位置C分别联系起来,可建立两个功能关系式:
1700978126
1700978127


1700978128
1700978129
1700978130
式中m为小球质量.由此可解得
1700978131
1700978132


1700978133
1700978134
1700978135
(2)小球在C2处的惯性离心力水平向右切向分量为
1700978136
1700978137


1700978138
1700978139
1700978140
C2处的最大静摩擦力和滑动摩擦力为
1700978141
1700978142


1700978143
1700978144
1700978145
因此小球到达C2点后不能停留在该处,而会朝右后退运动.
1700978146
1700978147
1700978148
1700978149
1700978150
力学(物理类) [:1700973459]
1700978151
力学(物理类) 3.4 碰 撞
1700978152
1700978153
宏观世界经常会发生物体间的碰撞,碰撞过程经历的时间一般很短,物体的动量却有明显变化,可见碰撞力很大,常规力(例如重力、地面摩擦力等)与其相比提供的冲量可以忽略,碰撞前后系统动量守恒.物体因运动到一起而发生碰撞,全过程物体间力的作用有可能不损耗系统动能,犹如其间是弹性力的作用,这样的碰撞称为弹性的,否则称为非弹性的.碰后物体一起运动,系统动能损失最大,称为完全非弹性碰撞.两个物体的碰撞为二体碰撞,自然也有多体碰撞.将碰撞的物体模型化为质点,碰撞前后各质点速度若都在一条直线上,称为一维碰撞;不在一条直线上,但在一个平面内,称为二维碰撞;再者,还有三维碰撞.一维碰撞也称为正碰撞,二维、三维碰撞为斜碰撞,第5章将述及质心参考系中的二体斜碰撞都是二维碰撞.
1700978154
1700978155
碰撞的基本问题是已知碰撞前系统的运动状态,要求确定碰撞后系统的运动状态.处理多体碰撞与斜碰撞时,将物体模型化为质点,常会丢失真实物体互相挤压和真实物体几何位形可提供的力学关系,使得碰撞问题的解出现不定性.这种情况下,物体可以不处理成质点.
1700978156
1700978157
微观粒子间的相互作用,也会使粒子彼此快速接近,继而快速分离.略去细节,同样可处理成碰撞过程.宇观星体间类似的接近、分离过程中,如果其他天体引力提供的冲量可以略去,也可处理成碰撞过程.
1700978158