1700978159
3.4.1 一维碰撞
1700978160
1700978161
质点1和2碰撞前后的状态分别在图3-25(a)(b)中示出,可为待求的碰后速度v1,v2建立动量方程:
1700978162
1700978163


1700978164
1700978165
1700978166


1700978167
1700978168
1700978169
图 3-25
1700978170
1700978171
为解v1,v2,还需建立补充方程.
1700978172
1700978173
●弹性碰撞
1700978174
1700978175
碰撞前后系统动能不变,补充方程
1700978176
1700978177
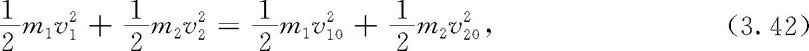
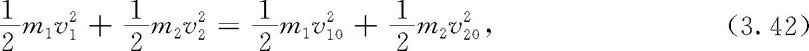
1700978178
1700978179
1700978180
与(3.41)式联立,数学上可得两组解,其一为v1=v10,v2=v20,物理上对应碰前运动状态;其二为
1700978181
1700978182


1700978183
1700978184
1700978185
物理上对应碰后速度.由上述解可得
1700978186
1700978187


1700978188
1700978189
1700978190
即碰后的分离速度大小等于碰前的接近速度大小,或者说碰撞前后相对速率大小不变.若m1=m2,据(3.43)式得
1700978191
1700978192


1700978193
1700978194
1700978195
即两者交换速度.台球桌上球1对准静止的球2打去,碰后球2被打走,球1却有可能停下,实现了运动状态的交换.弹性碰撞中,若m2≫m1,且v20=0,则有
1700978196
1700978197


1700978198
1700978199
1700978200
足球碰墙弹回,便属此例.
1700978201
1700978202
●完全非弹性碰撞
1700978203
1700978204
碰后质点1和2一起运动,可补充方程并得解
1700978205
1700978206


1700978207
1700978208