1700978209
可算得碰后动能损失
1700978210
1700978211


1700978212
1700978213
1700978214
●非弹性碰撞
1700978215
1700978216
介于弹性与完全非弹性之间的碰撞称为非弹性碰撞,此类碰撞可引入恢复系数
1700978217
1700978218


1700978219
1700978220
1700978221
来描述.(3.46)式联立(3.41)式,解得
1700978222
1700978223


1700978224
1700978225
1700978226
碰后动能损失量
1700978227
1700978228


1700978229
1700978230
1700978231
小于完全非弹性碰撞的动能损失量.
1700978232
1700978233
恢复系数e与物体结构有关,弹性碰撞的物体可以认为e=1,完全非弹性碰撞的物体可以认为e=0.
1700978234
1700978235
质点化三体一维碰撞前后运动状态如图3-26(a)(b)所示,动量守恒式为
1700978236
1700978237


1700978238
1700978239
1700978240


1700978241
1700978242
1700978243
图 3-26
1700978244
1700978245
若碰撞是完全非弹性的,补充方程
1700978246
1700978247
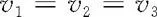
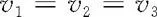
1700978248
1700978249
1700978250
后,便有唯一解.若碰撞是弹性的,补充方程
1700978251
1700978252


1700978253
1700978254
1700978255
后,v1,v2,v3解具有不定性.其中的原因在于将碰撞过程时间简略为零,真实物体在碰撞过程中互相挤压现象可提供的力学方程便都被略去了.物体没有了挤压,相当于刚性化,在此基础上进一步将物体质点化,于是就出现了解的不定性.
1700978256
1700978257
取一个简单的实例,三个相同的小球排成一直线,2和3号球彼此接触,1号球以v0速度朝2号球运动,如图3-27所示.真实情况必定是1与2号球接触部位的挤压早发生,2与3号球接触部位的挤压晚发生.后一挤压可能开始于前一挤压过程中,也可能开始于该过程之后.第二种情况相当于1与2间先发生二体碰撞,而后2与3间发生二体碰撞.这样的三体碰撞,实为二体碰撞的组合,给出各次二体碰撞特征,碰后三球速度有唯一解.在全弹性假设下,碰后v1=0,v2=0,v3=v0.如果将三个小球都刚性化,接触部位的挤压过程全部忽略,就会出现解的不定性.
1700978258