1700978259


1700978260
1700978261
1700978262
图 3-27
1700978263
1700978264
3.4.2 二维斜碰撞
1700978265
1700978266
两个质点的二维斜碰撞如图3-28所示,动量守恒方程为
1700978267
1700978268
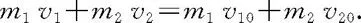
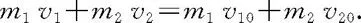
1700978269
1700978270
1700978271


1700978272
1700978273
1700978274
图 3-28
1700978275
1700978276
完全非弹性碰撞,可得唯一解
1700978277
1700978278


1700978279
1700978280
1700978281
若是弹性碰撞,补充方程
1700978282
1700978283
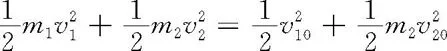
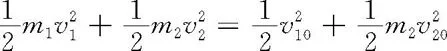
1700978284
1700978285
1700978286


1700978287
后,两个平面速度矢量v1和v2的解仍具有不定性.出现这种不定解的原因,也是物体的刚性化与质点化.某些二维弹性碰撞,给出物体的几何结构后,不仅二体,甚至多体问题都可能有唯一解(见习题3-24).回到两个质点的二维碰撞,若补充碰后某质点速度(例如v1)与平面上一个参考方向之间的夹角(例如图3-28中的),在弹性假设下,v1,v2均会有唯一解.
1700978288
1700978289
例11 采用第2章例7所取的二体约化质量方法,计算二体正碰撞过程中系统动能损失量.
1700978290
1700978291
解 碰撞过程中动能损失量E损由内力作功引起,因此在所有参考系中相同.正碰撞的两个质点在质点1参考系中,质点2以初速度v0对准质点1运动,碰撞后以速度v背离质点1运动,如图3-29(a)(b)所示.引入v=ev0,1≥e≥0,在质点1参考系中系统动能损失量为
1700978292
1700978293


1700978294
1700978295
1700978296


1700978297
1700978298
1700978299
图 3-29
1700978300
1700978301
其中μ即为二体约化质量.计算后可得
1700978302
1700978303


1700978304
1700978305
1700978306
转换到其他参考系,质点1,2初速分别记为v10,v20,则有
1700978307
1700978308

