1700981268
称为刚体相对于此转轴的回转半径.设想刚体质量m全部集中在与转轴相距的点部位,构成的假想质点相对于该转轴的转动惯量便是.各边长l的匀质长方体,相对于过中心转轴的回转半径.半径R的匀质球体,相对于过球心转轴的回转半径.
1700981269
1700981270


1700981271
例9 质点系动能Ek可分解为质心动能EkC与质点系相对质心动能之和,试据此导出刚体平行轴定理.
1700981272
1700981273
解 参考图5-17,设质量m的刚体绕固定轴MN的转动角速度为ω,转动动能便是
1700981274
1700981275


1700981276
1700981277
1700981278
质心速度和质心动能分别是
1700981279
1700981280


1700981281
1700981282
1700981283


1700981284
刚体相对于质心动能即为刚体在质心系中绕PQ轴的转动动能.刚体绕PQ轴转动角速度也是ω,故有
1700981285
1700981286


1700981287
1700981288
1700981289
由
1700981290
1700981291


1700981292
1700981293
1700981294
即得
1700981295
1700981296
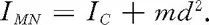
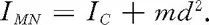
1700981297
1700981298
1700981299
例10 质量m,两边长分别为a和b的匀质长方板,相对于过中心O且与板面垂直轴的转动惯量I0,从量纲上考虑必可表达成
1700981300
1700981301


1700981302
1700981303
1700981304
其中α1,α2,α3是待定常数.
1700981305
1700981306
(1)利用匀质长方板可等分为两个小匀质长方板的特点,结合平行轴定理求解α1,α2,α3;
1700981307
1700981308
(2)利用垂直轴定理验证α1,α2,α3的正确性.
1700981309
1700981310
解 (1)将a,b置换后应有
1700981311
1700981312


1700981313
1700981314
1700981315
I0不会因a,b置换而变化,即得
1700981316
1700981317

