1700983682
1700983683


1700983684
1700983685
1700983686
(2)为联合①式消去②式中的x0,y0,先由①式得
1700983687
1700983688


1700983689
1700983690
1700983691
再代入②式,得二维速度场分布:
1700983692
1700983693


1700983694
1700983695
1700983696
这是一个不随时间变化的速度场.将④式代入③式,又可得二维加速度场分布:
1700983697
1700983698
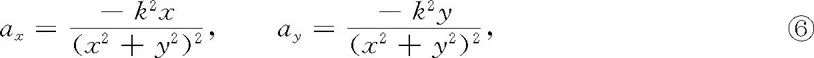
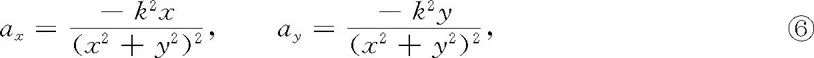
1700983699
1700983700
1700983701
是一个不随时间变化的加速度场.
1700983702
1700983703
利用正文(6.10)式,也可直接由⑤式导得⑥式.例如:
1700983704
1700983705


1700983706
1700983707
1700983708
(3)将二维速度场中的流线方程记为y=y(x),图6-15中(x,y)处切线的斜率一方面等于dy/dx,另一方面又等于vy/vx,即有
1700983709
1700983710


1700983711
1700983712
1700983713


1700983714
1700983715
1700983716
图 6-15
1700983717
1700983718
积分得
1700983719
1700983720
y=αx,α:不定常量.
1700983721
1700983722
对应的流线如图6-16所示.
1700983723
1700983724


1700983725
1700983726
1700983727
图 6-16
1700983728
1700983729
6.2.2 质量守恒和连续性方程
1700983730
1700983731
流动中流体的总质量应保持不变.在空间中取一区域,流体质量的守恒性表现为经由区域界面流出的流体质量等于区域内流体质量的减少量,这就是连续性方程.