1700986054


1700986055
时,d2Ep/dx2<0,x=0为不稳定平衡位置,
1700986056
1700986057


1700986058
时,d2Ep/dx2=0,x=0点平衡位置的稳定性待分析.
1700986059
1700986060


1700986061


1700986062
对于即情况下x=0平衡位置的稳定性,可以从环所受力Fx=-dEp/dx的分析进行讨论.结合①式,有
1700986063
1700986064


1700986065
1700986066
1700986067
设环心相对x=0位置偏离小量x,取泰勒展开到第4项,再保留到x3项,有
1700986068
1700986069


1700986070
1700986071
1700986072
这是一个回复性力,因此,
1700986073
1700986074


1700986075
时, x=0点仍是稳定平衡位置.
1700986076
1700986077


1700986078
(2)时,稳定平衡x=0位置附近的力Fx虽是回复性的,但不是线性的,形成的小振动不是简谐振动.
1700986079
1700986080


1700986081
时,稳定平衡x=0位置附近的力Fx可近似为
1700986082
1700986083


1700986084
1700986085
1700986086
略去x2高阶小量,可得
1700986087
1700986088


1700986089
1700986090
1700986091
这是一个线性回复力,环在x=0稳定平衡位置附近的小振动是简谐振动,角频率和周期分别为
1700986092
1700986093


1700986094
1700986095
1700986096
例16 试导出质点在位移三次方回复性保守力作用下的振动周期与振幅之间的关系,并给出位移三次方回复性保守力的两个实例.
1700986097
1700986098
解 位移三次方回复性保守力可表述为
1700986099
1700986100
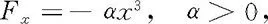
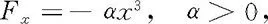
1700986101
1700986102
1700986103
质点可在x=0两侧往返运动.势能可表述为