1700989278


1700989279
1700989280
1700989281


1700989282
1700989283
1700989284
图 8-12
1700989285
1700989286
直尺相对S系运动过程中,首端A′,尾端B′分别与x轴上的x1,x2点重合时,S系中静止在x1,x2的两个时钟读数t1,t2恰好相同,运动直尺在S系中的长度便为
1700989287
1700989288


1700989289
1700989290
1700989291
为方便地利用t1=t2条件,取(8.7)中的第一式,可得
1700989292
1700989293


1700989294
1700989295
1700989296
即有
1700989297
1700989298


1700989299
1700989300
1700989301
这就是运动直尺长度收缩公式.需要注意,直尺的运动方向必须是它的长度方向.引申到一般物体的运动,应是物体中所有沿运动方向的线度均按(8.8)式缩短.运动速度越大,收缩后的线度越小,对于真实物体,零极限的线度是不可达的,因此速度可逼近c,但不能达到c.
1700989302
1700989303


1700989304


1700989305
前文图8-7中,由S′系讨论S系中一个时钟因相对S′系运动其计时率的变慢.为了显示运动时钟计时率变慢的相对性,图8-13中改为从S系讨论S′系中一个时钟P因相对S系运动其计时率的变慢.P与S系中静止在x1处的时钟相遇时,两者读数分别记为,t1,P与S系中静止在x2处的时钟相遇时,两者读数分别记为,t2.S系认为两次相遇事件之间的物理过程,由S系两个静止时钟测得的时间间隔为
1700989306
1700989307


1700989308
1700989309
1700989310


1700989311
1700989312
1700989313
图 8-13
1700989314
1700989315
而由相对S系运动的一个时钟P测得的时间间隔为
1700989316
1700989317


1700989318
1700989319
1700989320
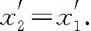
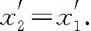
1700989321
P是一个运动时钟,它在S′系的静止位置是恒定的,故有选择(8.6)第四式,可得
1700989322
1700989323


1700989324
1700989325
1700989326
即有
1700989327