1700989328


1700989329
1700989330
1700989331
这就是运动时钟计时率变慢公式.
1700989332
1700989333


1700989334
运动时钟计时率变慢既是相对的,更是真实的.相对性含义已有较多的阐述,至此应当强调的是真实性.时钟的计时通常由某个动力学系统经历的周期性物理过程来实现,时钟相对S系运动时,S系认为它的计时率变慢了,S系还认为其原因必定是该动力学系统经历的周期性物理过程真实地变慢了.弹簧振子静止在S系中它的往返运动周期若为1秒,此振子以相对S系匀速运动时,振子“感觉”到自己的往返运动时间仍是1秒,S系却真实地观察到它的往返运动周期变慢为1.25秒.任何一个动力学系统测量自身物理过程所经历的时间间隔,即是用一个相对它静止的时钟测得的时间间隔,这样的时间间隔称为本征时间间隔,或简称为本征时间.T静>T动也可形象地说成系统的本征时间间隔因系统相对观察者运动而膨胀或者说延缓,简称时间膨胀或时间延缓.
1700989335
1700989336
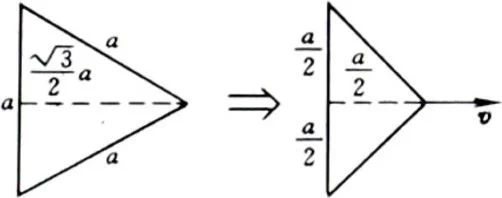
例6 静止时为等边三角形的三角板,以匀速度v作高速运动,v与板面平行.已知运动使三角板成为等腰直角三角形,试求v.
1700989337
1700989338


1700989339


1700989340
解 令原三角板沿着任意一条高的方向运动.设各边原长为a,高为如图8-14所示,运动时这条高的长为即有
1700989341
1700989342


1700989343
1700989344
1700989345

1700989346
1700989347
1700989348
图 8-14
1700989349
1700989350
得
1700989351
1700989352


1700989353
1700989354
1700989355
例7 已测得π+介子静止时的平均寿命为τ0=2.5×10-8S.实验室获得的某π+介子速度为(1-5×10-5)c,试求它可通过的平均距离l.
1700989356
1700989357
解 建立随π+介子一起运动的惯性系S′,在S′系中π+介子的平均寿命τ0可用一个静止时钟测得.实验室惯性系认为τ0是用一个运动时钟测得的,而π+介子在实验室的平均寿命τ则是需用两个静止时钟测得的,故有
1700989358
1700989359


1700989360
1700989361
1700989362
π+介子在实验室,可通过的平均距离为
1700989363
1700989364


1700989365
1700989366
1700989367
将已知数据代入后,即得
1700989368
1700989369


1700989370
1700989371
1700989372
例8 惯性系S中三艘已处于匀速直线运动状态的飞船1,2,3,各自的速度大小同为v,航向已在图8-15中示出.某时刻三艘飞船“相聚”(彼此靠近,但不相碰)于S系的O点,此时各自时钟都校准在零点.飞船1到达图中与O点相距l的P处时,发出两细束无线电信号,而后分别被飞船2,3接收到.
1700989373
1700989374


1700989375
1700989376
1700989377
图 8-15