1701048118
1701048119
设H是n维实线性空间,φ∶H→H是线性映射.任取H的一个基{ε1,ε2,…,εn},则有n阶方阵A,使得
1701048120
1701048121
(φ(ε1),φ(ε2),…,φ(εn))=(ε1,ε2,…,εn)A.
1701048122
1701048123
A的迹数(主对角线上元素之和)与基的选择是无关的,由φ所决定,称为φ的迹数,记作tr(φ).
1701048124
1701048125
定义8.1 设X是可剖分空间,f∶X→X是连续映射,规定f的Lefschetz数L(f)为
1701048126
1701048127


1701048128
1701048129
1701048130
定理8.5(Lefschetz不动点定理) 设X是可剖分空间,f∶X→X是连续映射.如果L(f)≠0,则f有不动点.
1701048131
1701048132
证明这个定理之前,先证两个引理.
1701048133
1701048134


1701048135
引理1(迹数可加性定理) 设H是有限维实线性空间,φ∶H→H是线性映射,H0是H的线性子空间,满足φ(H0)⊂H0.记是φ诱导的线性映射,φ0=φ|H0∶H0→H0,则
1701048136
1701048137


1701048138
1701048139
1701048140
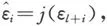
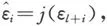
1701048141


1701048142
证明 记j∶H→H/H0为投射.取H的基{ε1,ε2,…,εn},使得{ε1,ε2,…,εl}是H0的基.记则是H/H0的基.设A是φ在{ε1,…,εn}下的方阵,则A有下面的分块形式
1701048143
1701048144


1701048145
1701048146
1701048147


1701048148


1701048149
其中A0是l阶方阵,它是φ0在{ε1,…,εl}下的矩阵;A1则恰为在下的矩阵.由迹数定义得结论. ▎
1701048150
1701048151
引理2(Hopf迹数引理) 设K是复形,{fq∶Cq(K;R)→Cq(K;R)|q∈Z}是链映射,则
1701048152
1701048153


1701048154
1701048155
1701048156
(f*q∶Hq(K;R)→Hq(K;R)是{fq}诱导的同调群线性映射).
1701048157
1701048158


1701048159


1701048160
证明 记和(K;R)都是fq的限制,则有交换图表:
1701048161
1701048162


1701048163
1701048164
1701048165
用引理1,得到
1701048166
1701048167

