1701048218
1701048219
3.证明射影平面到自身的任何连续映射都有不动点.
1701048220
1701048221


1701048222


1701048223
① Hn(Sn)和f*n都是要通过Sn的某个剖分(K,φ)来规定的,即Hn(Sn)=Hn(K),f*n=(φ-1fφ)*n∶Hn(K)→Hn(K).可以证明:deg(f)与(K,φ,)的选择无关,在此不详细论述了.
1701048224
1701048225
② 许多书中用有理系数同调群.
1701048226
1701048227
1701048228
1701048229
1701048230
基础拓扑学讲义 [:1701040242]
1701048231
基础拓扑学讲义 附录A 关于群的补充知识
1701048232
1701048233
我们假设读者已具备群的初步知识,包括群,同态,同构,子群,正规子群,商群,元素的阶,交换群(或称Abel群)等概念,以及循环群,自由循环群等具体例子.
1701048234
1701048235
本附录介绍本书中要用到的关于群的一些知识.主要是有限生成交换群的直和分解定理和秩,以及群的交换化.交换群中的运算称作加法,用“+”表示,单位元记作0,相应地把平凡群称作零群,平凡同态称作零同态,都记作0.
1701048236
1701048237
1.自由交换群与有限生成交换群
1701048238
1701048239
定义A.1 交换群F称为自由交换群,如果有子集A⊂F,使得∀x∈F可唯一表示成A中有限个元素的整系数线性组合:
1701048240
1701048241


1701048242
ai∈A,ni∈Z.
1701048243
1701048244
称A为F的一个基.
1701048245
1701048246
如果自由交换群F有一个基A只包含有限个元素,则称F是有限基自由交换群.
1701048247
1701048248
设A是自由交换群F的基,H是一交换群,则从A到H的任一对应θ∶A→H可按下式唯一决定同态φ∶F→H,
1701048249
1701048250


1701048251
1701048252
1701048253
称φ是θ的线性扩张.
1701048254
1701048255
定义A.2 如果交换群H有一有限子集
1701048256
1701048257
A={a1,a2,…,ar},
1701048258
1701048259
使得H的每个元素x可表成
1701048260
1701048261
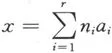
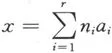
1701048262
1701048263
1701048264
的形式,则称H是有限生成交换群,称A是它们的一个生成元组.
1701048265
1701048266


1701048267
命题A.1 交换群H是有限生成的H是一个有限基自由交换群的商群.